Profile
Settings
Refer your friends
Sign out
What is inverse of 3 by 3 matrix?
A-1 is the inverse of Matrix for a matrix A. A simple formula may be used to determine the inverse of a 2 × 2 matrix. In addition, we must know the determinant and adjoint of matrix in order to compute inverse of a 3 × 3 matrix. The inverse of a matrix is another matrix that yields the multiplicative identity when multiplied with the given matrix.
The matrix inversion method uses the inverse of a matrix to find the solution to linear equations. Let’s look at the formula, techniques, and terminologies of inverse of matrix in this section.
The inverse of a matrix is another matrix that returns the multiplicative identity when multiplied with the given matrix. A-1 is the inverse of a matrix A, where A.A-1 = A-1A = I, where I is the identity matrix. An invertible matrix is one whose determinant is non-zero and for which the inverse matrix may be determined. The inverse of A =
Inverse Matrix Formula
The inverse of every real integer a was the number a-1, therefore a times a-1 equals 1. We understood that the reciprocal of a real number was the inverse of the number, as long as the number wasn’t zero. The inverse of a square matrix A, indicated by A-1, is the matrix, hence the identity matrix is the product of A and A-1. The resulting identity matrix will be the same size as matrix A.
For a matrix A, the inverse matrix formula is:
- A-¹ = adj(A)/|A|; |A| ≠ 0
where A is a square matrix.
Note: In order for the inverse of a matrix to exist, the following conditions must be met:
It is required that the provided matrix be a square matrix.
The matrix’s determinant should not be equal to zero.
Inverse of 3 × 3 Matrix
We know that there is an inverse matrix A-¹ for any non-singular square matrix A, such that A × A-¹ = I. Let’s look at any 3 × 3 square matrix that looks like this:
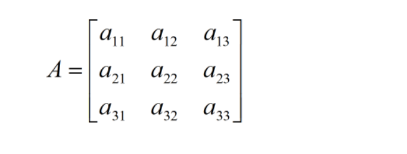
The inverse matrix formula, A-¹ = (1/|A|) Adj A, can be used to determine the inverse of a 3×3 matrix.
We’ll start by seeing if the supplied matrix is invertible, that is, if |A| ≠ 0. We may determine the adjoint of the supplied matrix and divide it by the determinant of the matrix if the inverse of the matrix exists.
The inverse of every n × n matrix can be found using a similar procedure. Let’s see if we can apply the same procedures to calculate the inverse of the m n matrix.
The inverse of an invertible matrix’s determinant is the inverse of the original matrix’s determinant. det(A-1) = 1 / det(A). Let us examine the evidence for the above assertion.
We know that, det(A • B) = det (A) × det(B)
Also, A × A-¹ = I
det(A •A-¹) = det(I)
or, det(A) × det(A-¹) = det(I)
Since, det(I) = 1
det(A) × det(A-¹) = 1
or, det(A-¹) = 1 / det(A)
Hence, it is proved.
Important Points on Inverse of a Matrix:
Points to Remember About Inverse of a Matrix:
The following principles will help you grasp the concept of inverse matrix more fully.
If an inverse of a square matrix exists, it is one of a kind.
(AB)-¹ = B-¹ A-¹ if A and B are two invertible matrices of the same order.
Only if the determinant of a square matrix A is non-zero, |A| ≠ 0, does the inverse exist.
When a row or column’s elements are multiplied by the cofactor elements of any other row or column, the result is zero.
The product of the determinants of two matrices is the product of the determinants of the two matrices separately. |AB| = |A|.|B|
3×3 Matrix Multiplication:
Three rows and three columns make up a 3×3 matrix. Each of the three rows of the first matrix is multiplied by the columns of the second matrix, and then all the pairs are added. A and B, for example, are two matrices such that:
Consider two 3 × 3 matrices A and B to better comprehend the multiplication of two 3 × 3 matrices.
Conclusion:
Matrices aid in the solution of linear equations. Matrices are incredibly valuable items that may be found in a variety of settings. The usage of matrices in mathematics may be found in a wide range of scientific and mathematical subjects. Almost every element of our life is influenced by engineering mathematics.
