Introduction
Polygons are the closed figures made by joining line segments end to end. It is a two-dimensional figure (only has length and breadth). The line segments which form a Polygon are called sides or edges. A polygon can have infinite sides. As you read above a polygon can have infinite sides, here are some examples of polygons that will clear your understanding of polygons. Examples- Triangle, Square, Rectangle, Heptagon, etc.
On the end, where sides are joined, there are the angles of the polygon.
TYPES OF POLYGON
There are basically four types of polygon
- Regular
- Irregular
- Convex
- Concave
Here is the basic understanding of these types of a polygon.
Regular Polygon: Regular Polygons are those which have all sides with interior angles equal. For example- Square, Rhombus, Regular Pentagon, Equilateral Triangle, etc.
Irregular Polygon: In the case of Irregular Polygons, Interior angles, Sides, are different. For example- Scalene Triangle, A kite, etc.
Convex Polygon: All convex polygons have all interior angles less than 180◦ and this is a necessary condition that will apply to all angles of a polygon. These are called convex because their vertex comes outward from the center of the shape.
Concave Polygon: In Concave Polygon, at least an interior angle of a polygon is greater than 180◦ . And these polygons have at least four sides. Now, why are they called Concave Polygons- it is because their vertex goes inward towards the center of the shape.
Do you know anything about Interior angles of Polygon?
Above we talked a little about the introduction of Interior Angles. Here, we will discuss them in detail.
The angle formed by adjacent sides is known as the Interior Angle of the Polygon. As the name suggests, interior angles so this angle will form inside of adjacent sides of Polygon.
Sum of Interior Angles of A Polygon
As you may know, the sum of Interior angles of a triangle is 180◦. So, same as triangles we have a formula for finding the sum of interior angles of a polygon.
Sum of Interior angles = (s-2)x 180 degrees
s = Number of sides of polygons
For example, for a polygon having 7 sides the sum is, n = 7
Sum = (7 -2 ) × 180
sum = 900 degree
Polygon | No. of sides of a polygon | Sum Of Interior angles (in degrees) |
Triangle | 3 | 180 |
Quadrilateral | 4 | 360 |
Heptagon | 7 | 900 |
Nonagon | 9 | 1260 |
Decagon | 10 | 1440 |
Interior Angles Theorem
Statement: The sum of interior angles of a polygon is (2n-4) × 90 degrees. where n is the number of sides of a polygon.
Proof: Consider an n side polygon ABCDEF, and any point O within the polygon such that OA, OB, OC are joined together.
An n-sided polygon will form n triangles in it. As we know, the sum of interior angles of a triangle is 180 degrees, so n triangle will give n * 180 degrees sum.
So, Total Angles in the interior + sum of angles in the interior = 2 – n*90
———–eqn (1)
At Point O, the sum of all angles is 360 degrees.
On substituting the above values in Eqn 1 we get,
360 degrees + 2n * 90 degrees = total interior angles of a polygon
Therefore, the Sum of interior angles = (2n*90) – 360 degrees
take 90 as common,
Sum of all inner angles = (2n – 4) * 90 degrees
Interior Angles Formula
We have three methods to calculate the formula of interior angles
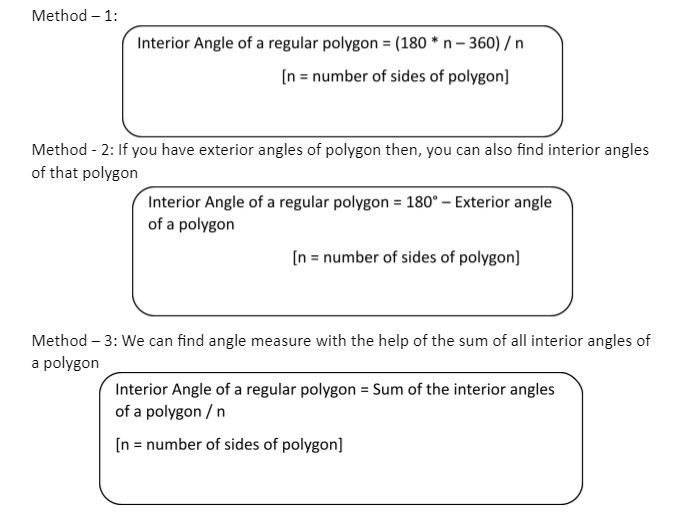
Some regular polygons with their interior angles
Regular Polygon | A measure of interior angles (in degrees) |
Triangle | 60 |
Quadrilateral | 90 |
Pentagon | 108 |
Heptagon | 128.57 |
Octagon | 135 |
Decagon | 144 |
Interior angles of a convex polygon
As mentioned above, the Convex polygon has all angles less than 180 degrees.
So, all interior angles of a polygon are less than 180 degrees.
The formula for finding the sum of interior angles,
Sum = (n – 2) × 180 degrees
where n is the number of vertices present in a convex polygon.
Conclusion
You get to know about the interior angles of polygons in detail. Interior angles are used in higher mathematics in many places. Interior angle is the angle formed between adjacent sides of a polygon. We have also seen what is the interior angle theorem and what is the interior angle formulas.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






