The equation of a line expressed in the intercept form is written as x/a + y/b = 1. This is a significant version of an equation that can be written for a line. Additionally, the signs of the intercepts in this equation provide information that assists us in determining the location of the line in relation to the axes that are being used to coordinate the data. The intercept form of the equation of the line can be regarded as the line that produces a right triangle with the coordinate axes, with the lengths of the sides being represented alternately as ‘a’ units and ‘b’ units.
Intercept Form
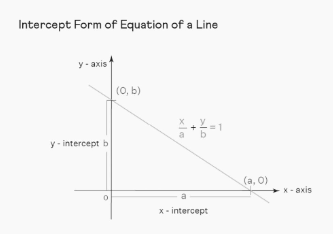
The x-intercept is denoted by the letter a, and the y-intercept is denoted by the letter b. The equation for the intercept form of the equation of a line is written as x/a + y/b = 1. The x-intercept is the point on the x-axis that is the shortest distance from the origin to the point where the line cuts the x-axis, and the y-intercept is the point on the y-axis that is the shortest distance from the origin to the point where the line cuts the y-axis. Both of these are referred to as the origin. Taking into consideration the points as well, the line crosses the x-axis at the point where it is equal to zero, and it crosses the y-axis at the point where it is equal to a. (0, b).
The equation of a line in intercept form reads as follows: x/a + y/b = 1.
The variables in this equation are denoted by x and y, whereas a and b represent the x-intercept and the y-intercept, respectively, in the equation. This equation has a slope of negative b over positive a.
As a result of the fact that this line traverses both of the coordinate axes, it forms a right triangle with the axes, and the area of the right angled triangle is equal to the product of half of its intercepts, which is denoted by the notation 1/2 |ab|. In addition, the intercept form of the equation of a line can be simplified into the standard form of the equation of a line, which is represented as bx + ay = ab. This is because the standard form of the equation of a line is a linear equation.
A Graph Showing the Intercept The Equation in Its Form
The coordinate axes are cut in the graph of intercept form at the two spots that are respectively located on the x-axis and the y-axis. The two locations are located on the x-axis and the y-axis, respectively, and are a distance of a units and b units away from the origin, respectively. Due to the fact that the line cuts an intercept of ‘a’ units on the x-axis, it travels through the point on the x-axis that is represented by the coordinates (a, 0). Additionally, it cuts an intercept of ‘b’ units on the y-axis, and it passes through the point (0, b) on the y-axis correspondingly.
Formulation of the Equation in the Form of an Intercept
The intercept form of the equation of the line is one of the forms of a line’s equation that may be derived from the other forms of a line’s equation. The two-point form of the equation of a line is used here as a starting point for deriving the intercept form of the equation of a line.
Form with Two Points
In order to solve an equation for a line using the two-point form, you need to choose two points along the line. Using the two-point version of the equation of a line, one can determine the equation of a line that passes through the two points (a, 0) and (0, b). The following expression is the equation of the line that passes through the two points (a, 0) and (b, 0) respectively.
y – 0 = (b – 0)/(0 – a).(x – a)
y = b/-a.(x – a)
-ay = b(x – a)
-ay = bx – ab
ab = bx + ay
bx + ay = ab
(bx + ay)/ab = 1
bx/ab + ay/ab = 1
x/a + y/b = 1
Notes Crucial Concerning the Intercept Form
The following ideas are helpful in comprehending the specifics of the intercept form of an equation for a line in a straightforward and concise manner.
- The equation of a line expressed in the intercept form is written as x/a + y/b = 1.
- When writing the equation of a line using the intercept form, the x-intercept is given in units of a, and the y-intercept is given in units of b.
- We are able to determine the quadrants that the line travels through based on the sign of the intercepts.
- The intercept form of an equation for a line, in which the coordinate axes are used to build a right triangle, has an area 1/2 · |ab|.
Conclusion
The x-intercept is denoted by the letter a, and the y-intercept is denoted by the letter b. The equation for the intercept form of the equation of a line is written as x/a + y/b = 1. The x-intercept is the point on the x-axis that is the shortest distance from the origin to the point where the line cuts the x-axis, and the y-intercept is the point on the y-axis that is the shortest distance from the origin to the point where the line cuts the y-axis.When writing the equation of a line using the intercept form, the x-intercept is given in units of a, and the y-intercept is given in units of b.We are able to determine the quadrants that the line travels through based on the sign of the intercepts.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






