Profile
Settings
Refer your friends
Sign out
It is a part of calculus mathematics that uses a part to find the whole by uniting them. Integration can be used to find volumes, areas, central points, and many other useful things. But adding up all the little pieces is tedious, so we just reverse the process of differentiation.
Trigonometric functions
In mathematics, trigonometric functions help us find a relationship between an angle of a right-angled triangle with the sides of the triangle. If there exists a right-angled triangle , then there are six basic trigonometric functions,
Trigonometric identities
Trigonometric identities are equations involving trigonometric functions that holds equality for all values of the variables included. Some of the most used trigonometric identities in integration are,
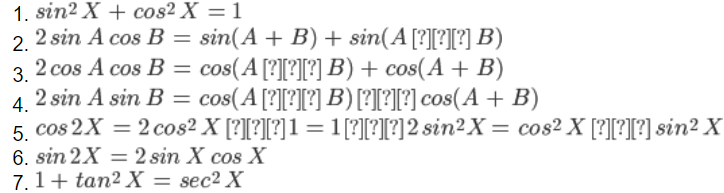
Trigonometric substitutions
Some of the most common trigonometric substitutions used in integration are
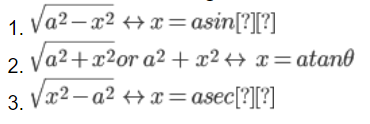
Types of trigonometric integration
Integration involving the use of trigonometric identities
We have complex trigonometric functions in the question in these types of problems which are hard to deal with. So we break it down into more specific trigonometric functions. For example, let us take the following question,
Integration involving the product of a sine and a cosine functions
In these types of problems, we deal with questions that have a product of sine and cosine functions. Although it seems like any other type of trigonometric function, it is a particular case. Standard solving methods get very lengthy in this case, so there are predefined formulas for it.
Integration involving trigonometric substitution
In these types of problems, we substitute functions in other variables with functions in trigonometric variables. It helps to simplify the problems and makes solving them easier and faster.
For example,
Conclusion
In our daily lives, integration is used in many important places. Engineers use it to predict the shape of a building; physicists use it to find the centre of gravity of things and many more uses. Trigonometry in integration makes it easier, faster, and more effective.
