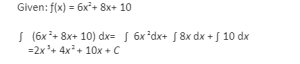Profile
Settings
Refer your friends
Sign out
Integration Definition
If f'(x) = g(x), a function f(x) is called an integration, integral, primitive, or anti-derivative of a function g(x)..
Integral of the function refers to the process of determining an indefinite integration of a given function.
Integration is the inverse of Differentiation and is a very important aspect of Calculus.
Basic examples of Integration rules.
If y = 2x + 7
or y = 2x – 8
or y = 2x + 100000
then for all cases dy/dx = 2
Hence we can say that anti-derivative or
integral of 2 is 2x + C
where C = any real constant.
Rules:
Power Rule:
Integration’s power rule is the inverse of differentiation’s power rule.
The indefinite integral of a variable raised to a power is obtained.
The indefinite integral of a variable raised to a power is obtained. Here’s an example of the power rule:
The fact that we can apply the power rule to get the indefinite integral of a function is not always clear.
Let’s say we wish to calculate the indefinite integral of the formula 3x. It’s not difficult at all. All we have to do now is change the expression to raise x to a higher power. The nth root of a number a can be expressed in index form (that is, as a raised to a power) using the following formula:
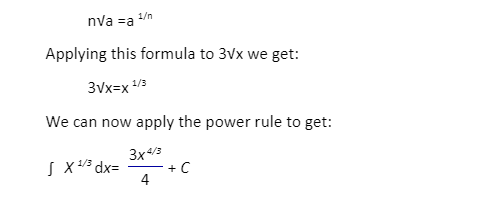
Constant co-efficient Rule:
The constant-coefficient rule (also known as the constant multiplier rule) states that the indefinite integral of c(x), where c is a constant coefficient and (x) is a function, is equal to the indefinite integral of (x) multiplied by c.
This can be stated formally as follows:
The constant-coefficient rule effectively allows us to integrate the rest of an expression while ignoring the constant coefficient. Let’s say we wish to calculate the indefinite integral of the formula 5x ². The indefinite integral of this equation is equivalent to the indefinite integral of x²multiplied by five.
According to the constant-coefficient rule:
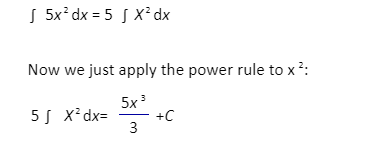
Sum Rule:
The sum rule describes how to combine functions that are the sum of multiple terms. It basically says that we should integrate each term in the sum separately before combining the results. It makes no difference in whatever order the terms appear in the outcome.
This can be stated as:
It’s crucial to remember that each term in a function that’s the sum of two (or more) terms can be considered a function in its own right, even if it’s a constant term. Let’s say we wish to find the polynomial function’s indefinite integral. ƒ(x) = 6x²+ 8x+ 10. Applying the sum rule, we get:
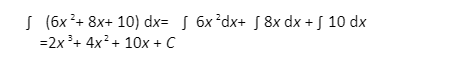
Difference Rule:
The difference rule explains how to combine functions that require two or more terms that differ. It works similarly to the sum rule in that it instructs us to integrate each term in the sum independently.
The main distinction is that the order in which the terms appear is crucial and cannot be modified. This rule can be stated in formal terms as follows:
Integration Formulas of Trigonometric functions:
Integration is the process of locating the integral. Here are a few key integration formulas to remember for quick and accurate calculations. When dealing with trigonometric functions, we simplify them and rewrite them as integrable functions.
A list of trigonometric and inverse trigonometric functions is provided below.
- ∫ cosx.dx = sinx + C
- ∫ sinx.dx = -cosx + C
- ∫ sec2x.dx = tanx + C
- ∫ cosec2x.dx = -cotx + C
- ∫ secx.tanx.dx = secx + C
- ∫ cosecx.cotx.dx = -cosecx + C
- ∫ tanx.dx =log|secx| + C
- ∫ cotx.dx = log|sinx| + C
- ∫ secx.dx = log|secx + tanx| + C
- ∫ cosecx.dx = log|cosecx – cotx| + C
Integral of Square Root:
We will use the formula ∫xn dx = x n+1/(n + 1) + C by substituting n = 1/2 in it as √x is nothing but x raised to the power of one by two, that is, √x = x ½ Therefore, we have
Conclusion:
Functions, differentiation, and integration are only a few examples of calculating procedures. Integrals are used in a variety of domains, including mathematics, science, and engineering.
In addition, we mostly use integral formulas to calculate areas or irregular forms in a two-dimensional space.Integrals are used in mathematics to find the following:
- The centre of mass (Centroid) of an area with curved sides.
• The curve’s average value.
• The space that exists between two curves.
• The space beneath a curve.
Integrals are used in physics to find the following:
- Center of gravity.
- Center of mass.
• Vehicle mass and moment of inertia
