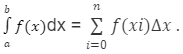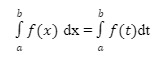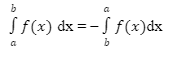Integration is a way to find the whole part together. Integral Calculus finds a function for which the derivative is given. Integration is the opposite of differentiation. Integral is used to define and calculate the area of the area enclosed by the function graph. The area of a curved shape is estimated by tracing the number of sides of the polygon carved into it. This process, known as the depletion method, was later adopted as an integration. There are two forms of integrals, definite integrals and definite integrals. Differentiation and integration are the basic tools of calculus used to solve mathematical and physics problems. The principles of integration were developed by Leibniz.
Integration is the process of finding the area below the curve. This is done by drawing as many small rectangles as possible to cover that area and summing those areas. The sum approaches the limit equal to the area under the curve of the function. Integration is the process of finding an indefinite integral of a function. If the function is integrable and its integral is finite in the domain with the specified limits, it is a definite integral problem.
If d / dx (F (x) = f (x), then ∫f (x) dx = F (x) + C. These are indefinite integrals. For example, f (x) = x³ is the derivation of the following function Let f (x) be f` (x) = 3x², and the indefinite integral of 3x² is f (x) = x³.
Therefore, we can see that the derivative of F (x) = f (x) is not unique, but the indefinite integral of f (x) is unique. The indefinite integral of f (x) is an infinite family of functions. The standard formula for integration is meaningful only if the integrand is specified in “standard” form. Most physical applications or analytical purposes require advanced integration techniques that analytically reduce the integrand to a convenient and resolvable form.
Standard Integrals:
Integral is a basic operation of integral calculation. Differentiation has simple rules for finding derivatives of complex functions by differentiating simpler component functions, but integration does not, so a table of known integrals is often useful. This page lists some of the most common indefinite integrals.
Formula of Definite integral:
Given a continuous function f (x) in the interval [a, b], divide the interval into n subintervals of equal width Δx and select points from each interval x ∗ i. In that case, the definite integral of (x) goes from a to b is
Evaluating definite integrals in this way can be very tedious due to the complexity of the calculation. In the second half of this chapter, we will develop a method for calculating definite integrals without taking the range of Riemann sum. However, for now, you can rely on the fact that definite integrals represent the area under the curve, and you can use geometric formulas to evaluate definite integrals and calculate their area. This is done to make sure that a particular integral represents a region. Therefore, we will explain what to do if the curve of the function falls below the x-axis.
Properties of Definite Integrals
A particular integral is about the accumulation or sum of a quantity and is closely related to the indefinite integral. They are from pure mathematics using geometric applications such as surface and volume, to the mass of an object, the work done, or, to name a few, the pressure exerted on an object.
The definite integral of the function 𝑓 (𝑥) from 𝑥 = 𝑎 to 𝑥 = 𝑏 can be interpreted as the signed region under the 𝑓 (𝑥) curve from 𝑥 = 𝑎 to 𝑥 = 𝑏.
- The variable 𝑥 that appears in the definite integral is called a dummy variable and can be replaced with another variable to get the same result.
- We can interchange the limits on any definite integral, all that we need to do is take a minus sign onto the integral when we do.
- The definite integral gives the signed area under the curve equal to the area of the rectangle of length | 𝑐 | and | 𝑏 − 𝑎 |, up to the character.
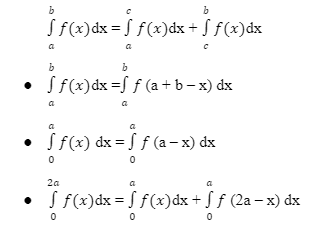
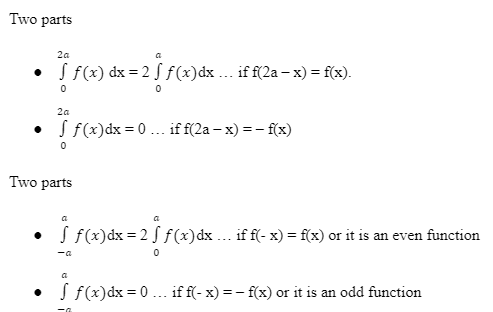
Conclusion:
The properties of integrals help solve integral problems. Integration with functions and algebraic expressions. These problems can be solved with a complete understanding of the properties of integrals. The properties of integrals can be broadly classified into the following two types according to the type of integral.
- Properties of indefinite integral
- Specific integral characteristics.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out