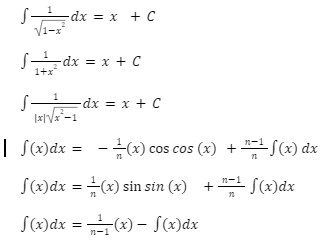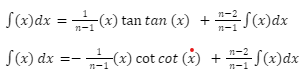INTEGRATION OF FUNCTIONS

Integration is the reverse process of differentiation. It is the process of finding the function from its derivative. In integration, we study the area under the curve. Integrals are of two types – the first is definite integral and the second is indefinite integral. The integration of functions includes formulas such as basic integrals, integration of trigonometric functions, etc. Here you will study how to calculate the integration of function, standard formulas, and what is the use of integration in our day-to-day life.   

INTEGRATION OF THE FUNCTION-

Integration is the most fundamental tool in calculus. As we know, there are two types of integrals- definite and indefinite integrals. The need for integral calculus arises for solving a function when its derivative is given or to find the area bounded by the graph of a function under certain conditions. It can be calculated by drawing rectangles under the curve and adding those areas.

Indefinite and definite integrals are connected by the Fundamental Theorem of Calculus, which makes integration a practical tool for science and engineering.

RELATION BETWEEN INTEGRATION AND DIFFERENTIATION OF A FUNCTION-

Integration of a function is a method to solve the function from its differentiation. Instead of differentiating a function, you are given the derivative of a function and asked to find its original function. Such a process is called integration or anti-differentiation.

The important rule to remember is that the integrals and derivatives are the opposite.

PROPERTIES OF INTEGRATION-

There are various properties of integration to be kept in mind in order to solve the integration of function. Here, a few of them are listed below-

1. The process of differentiation and integration are opposite of each other.        

d / dx∫fxdx=f(x)  and  ∫f’xdx=fx+C

 Where C is any constant.

2. Sum

∫ fx+gxdx=∫fxdx+∫gxdx

3. For any real number k,

∫k fxdx=k∫fxdx                         

There are certain rules to calculate the integration of a function- 

Difference Rule-

 ∫fx-gxdx=∫fxdx-∫gxdx

Power Rule-

∫xndx=xn+1n+1+C  where n ≠ -1

Exponential Rule-

 ∫exdx=ex+C

 ∫axdx=axln a +C

 ∫ln⁡(x)dx=x lnx-x+C

Reciprocal Rule-

 ∫a dx=ax+C, where a is constant

Constant Multiplication Rule-

 ∫a dx=ax+C, where a is constant.

STANDARD INTEGRALS-

  1.dx=x+C

  ∫a. dx=ax+C

  ∫xn.dx=[xn+1(n+1)]  +C ,  n≠1

  ∫1x dx=ln x +C

 INTEGRATION FORMULA OF TRIGONOMETRIC FUNCTIONS-

 Here is a list of trigonometric and inverse trigonometric functions. It is used for speedy calculation.

• ∫sinx dx=-cosx+C

• ∫cosx dx=sinx+C

• ∫cosec2x dx=-cotx+C

• ∫x dx=tanx+C

• ∫secx tanx dx=sec x+C

• ∫cosecx cotx dx=-cosecx+C

• ∫tanx dx=log secx +C

• ∫cotx dx=logsinx+C

• ∫cosecx dx=log cosecx-cotx +C

• ∫secx dx=log secx+tanx +C

INTEGRATION FORMULAE-

INTEGRAL FORMULAE FOR SOME SPECIAL FUNCTIONS-

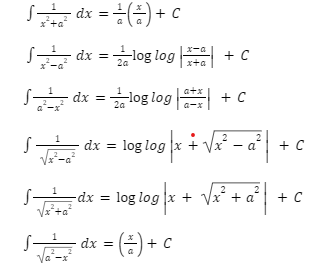
METHODS OF INTEGRATION-

There are various methods to perform the integration of the function-

1. Integration by parts

2. Integration by substitution 

3. Integration by partial fraction

Let us talk about the method separately, 

1. Integration by parts-

Let f and g be any two differentiable functions of single variable x. Using the product rule of differentiation, 

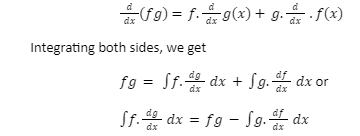
Integration of product  two function= (first function) *(Integral of the second function)- Integral of        [(differential coefficient of the first function)* (Integral of the second function)]

2. Integration by substitution-

The given integral ∫f(x) dx can be transformed into another form by changing the independent variable x to t by substituting x=g(t).

Let I = ∫f(x) dx

Putting x= g(t), so that dxdt=g'(t)

 dx=g’tdt

 Hence, I = ∫fxdx= ∫fgtg’tdt

3. Integration by a partial fraction-

The ratio of two polynomials in the form of  PxQx , where P(x) and Q(x) are a polynomial of x and Q(x)≠0 is called a rational function.

If the degree of P(x) › degree of Q(x), then the rational function is improper.

If the degree of P(x) ‹  degree of Q(x), then the rational function is proper.

The rational improper function can be reduced to proper rational functions by the long division method. 

CONCLUSION-

By the method of integration, it has become very easy to calculate the area of any given curve. The above-mentioned formulas have made the calculation of integration very easy. Integration is a process that is the reverse of differentiation. 

Let ddxFx=fx

Then, ∫fxdx=Fx+C , where C is constant of integration

 From the point of view of geometry, the indefinite integral is the collection of a family of curves, each of which is obtained by translating one of the curves parallel to itself upwards or downwards along the y-axis.