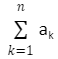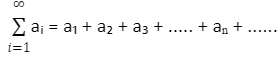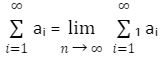Infinite Series

In mathematics, a series can be defined as the process of adding an endless number of numbers or quantities to a specific starting number or amount over and over again. Series are used in many fields of mathematics, including the study of finite structures, such as combinatorics, which is used in the formation of functions. The study of series is essential for understanding calculus and its generalisation, as well as for understanding mathematical analysis. Beyond their use in mathematics, infinite series are also widely employed in a variety of quantitative sciences such as statistics, physics, computer science, finance and other related fields. 

Series definition

On the basis of the concept of sequences, we can define series in mathematics. Due to the fact that sequence and series are linked concepts. For example, suppose that the sequence of numbers a₁, a₂, a₃,……a_n is such that the formula a₁ + a₂ + a₃ +……+ a_n is known as the series associated with the given sequence. Depending on whether the provided sequence is finite or infinite, the series is either finite or infinite, and vice versa. Series are frequently stated in a compact form, known as sigma notation, in which the Greek letter sigma ‘∑’ is used to denote the summation that is being performed.

This is how we can abbreviate the series of numbers a₁ + a₂ + a₃ +……+ a_n as

Series number 

An infinite series may have a large number of terms in the form of numerical values or functions or quantities, among other things. When the series is presented, it refers to the symbolised amount rather than the total in its entirety. For example, 2 + 4 + 6 + 8 + 10 + 12 is a series of six words that is represented by the number 2. This is accomplished by employing the phrase “sum of a series,” which refers to the number that is obtained by summing the terms of the series; in this case, 42 is obtained by adding the terms of the series together. 

General representation of a series

Using the pattern of terms in the series, we can get the general term for the group of terms in question. According to the preceding example, the general term is a_n = 2n, and the sum of this series can be calculated as follows:

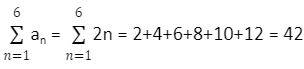
However, depending on the number of terms in the series, we can divide it into two categories: finite and infinite. 

Finite series

A finite series is a series of terms that has a countable number of terms in it.

Assume that the series a₁ + a₂ +…+ a_n has n terms and that the series contains at least one term from each of the other series.

As a result, S_n is the sum of the series, and it is denoted as follows: 

S_n = ∑ a_n

As an additional option, we can define the total of a specified number of terms. These are conveyed in the following ways: 

S₁ = a₁

S₂ = a₁ + a₂

S₃ = a₁ + a₂ + a₃

S₄ = a₁ + a₂ + a₃ + a₄

….

S_n = a₁ + a₂ + a₃ + … + a_n

Infinite series

An infinite series is a succession of phrases that has an infinite number of possible outcomes. This can be represented as follows: 

The index of summation is denoted by the letter “i” in this case.

To denote the index of summation, we can use a variety of different letters. 

All of these representations are identical to each other.

We are unable to carry the infinite string of additions mentioned by a series in any practical manner. Another option is to limit how many terms and finite sums are represented, making it possible to assign a value to a string that is known as the sum of the series in some cases. If the limit exists, then the value of the limit is the limit as n tends to infinity the finite sums of the n first terms of the series, which are referred to as the nth partial sums of the series, are called the nth partial sums of the series. 

If this limit is present, the series is said to be convergent or sumizable. In other words, the series can be totalled. Otherwise, this series is called a divergent series. In the above representation, the limit is called the sum of the series. 

Sum of infinite series formula 

It is not possible to define the sum of infinite for an arithmetic series, because the sum of terms tends to the value 0.

When |r| is greater than one, the sum to infinity for a geometric series is also undefined.

If |r| is less than one, it is possible to calculate the sum of a geometric series to infinity.

As a result, the sum of infinite series can be calculated using the following formula: 

S_∞ = a/1-r 

Or, lim_n→∞ S_n = S_∞ = a/1-r 

Conclusion 

In engineering, physics, computer science, finance, and mathematics, infinite series have a wide range of applications. They are used in engineering to analyse current flow and sound waves, among other things. In physics, infinite series can be used to determine how long it takes a bouncing ball to come to rest or how long it takes a swinging pendulum to come to a complete halt.