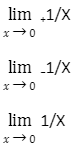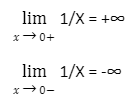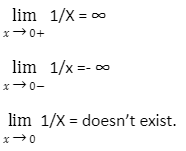It explains us that anytime x approaches a, f(x) is a huge negative number, and that the value of f(x) drops without bound as x approaches a. Warning: when we say a limit Equals, the limit technically does not exist. Only if L is a number does Lim x→a f(x)=L make sense (technically).
Definition:
Evaluating a function’s limit at a point, or evaluating a function’s limit from the right and left at a point, allows us to characterise a function’s behaviour around a specific value. We can also characterise the behaviour of functions with no finite limits, as we will demonstrate.
The third and last function introduced at the beginning of this section, h(x)=1/(x-2)² is now our focus. We can see from the graph that as x approaches 2, the values of h(x)=1/(x-2)² become larger and larger until they reach infinity. The limit of h(x) as x approaches 2 is positive infinity, according to mathematics. We express this concept symbolically as
Properties:
The following is a list of key infinity attributes.
Addition Property:
When any integer is multiplied by infinity, the result is infinity.
- ∞ + ∞ = ∞
- -∞ + -∞ = -∞
Multiplication Property:
When a number is multiplied by infinity, the product’s value is infinity as well.
- ∞ × ∞ = ∞
- -∞ × ∞ = -∞
- -∞ × -∞ = ∞
Some Special Properties:
If x is a positive integer, then
- + (-∞) = -∞
- X + ∞ = ∞
- X – (-∞) = ∞
- X – ∞ = -∞
For x > 0:
- X × (-∞) = -∞
- X × ∞ = ∞
For x < 0:
- X × (-∞) = ∞
- X × ∞ = -∞
Find Infinite Limits:
We need to understand f as x’s behaviour. In this part, we establish infinity limits and demonstrate how they alter the graph of a function.
First, we’ll look at what it means for a function to have a finite limit at infinity. The concept of a function having an unlimited limit at infinity is then explored. We looked at vertical asymptotes in Introduction to Functions and Graphs; in this section, we’ll look at horizontal and oblique asymptotes.
Infinite Limits Examples:
Example 1: Consider each of the following restrictions.
Solution: So we’ll look at some one-sided limitations as well as the typical limit here. We can’t just enter x=0 in any of the three circumstances. We’d get divided by zero if we did. Remember that the definitions above can simply be adjusted to get comparable definitions for the two one-sided limits that we’ll require.
There are numerous approaches we could use to obtain values for these limits. Plugging in some points and seeing what value the function approaches is one method. We mentioned in the last part that we wouldn’t do this anymore, but in this case it’s a good method to show what’s going on with this function.
So, here’s a table with x values from both the left and right sides. We can estimate the value of the two one-sided limits using these values, and once we’ve done so, we can exploit the fact that the normal limit exists only if the two one-sided limits exist and have the same value.
x | 1/x | x | 1/x |
-0.1 | -10 | 0.1 | 10 |
-0.01 | -100 | 0.01 | 100 |
-0.001 | -1000 | 0.001 | 1000 |
-0.0001 | -10000 | 0.0001 | 10000 |
We can see from this table that when we make x smaller and smaller, the function 1/x grows larger and larger while maintaining the same sign as x. It should be obvious that this pattern will continue for any smaller x value we choose. The function consists of a constant (in this example one) divided by a decreasing number. As previously stated, the resulting fraction should be an increasing number with the same sign as x.
For any x sufficiently close to zero, we can make the function as large and positive as we like while remaining positive (i.e. on the right). Similarly, for any x sufficiently close to zero, we can make the function as huge and negative as we wish while remaining negative (i.e. on the left). So, based on our definition above, the two one-sided limits should have the following values.
Graphing the function is another approach to see the values of the two one-sided limits. We indicated in the previous part that we won’t do this very often because most functions aren’t something we can just draw down quickly, and there are issues with reading values off the graph. However, it is not difficult to draw a graph of the function in this situation, and as we will see, accuracy is not a concern. So, here’s a rough drawing of the graph.
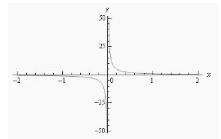
As we can see from the graph, the function behaves almost exactly as we projected based on our table data. The larger (in the positive sense) the function becomes as x approaches zero from the right, while the larger (in the negative meaning) the function becomes as x approaches zero from the left.
Finally, because the two one-sided limits have different values, the normal limit will not exist in this case.
In conclusion, the values of the three limits for this example are as follows.
Conclusion:
This is essentially saying the same thing as the maths above. If ‘x’ (1 billion) is a large quantity in comparison to ‘a’ (48 cents), then x + a (1 billion dollars and 48 cents) can be treated as x. (1 billion dollars).
One of the most common uses of infinite limits is to figure out which pieces of information contribute the most to the solution when dealing with large complex functions. This enables us to simplify problems to the point where they can be solved. Rounding is the everyday use of infinite limits, with important applications in maths and science.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out