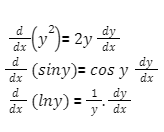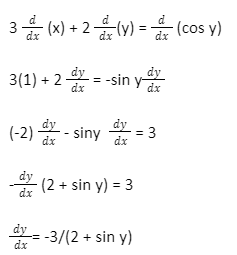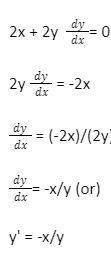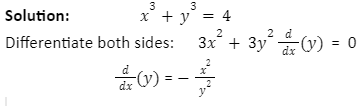The process of obtaining the derivative of an implicit function is known as implicit differentiation. The 2 types of functions are explicit and implicit functions. In explicit function y = f(x), the dependent variable ‘y’ is on one side of the equation .It is not, however, necessary to have ‘y’ on one side of the equation. Consider the following functions, for example:
x2 + y = 2
xy + sin (xy) = 0
Even though ‘y’ is not side of the equation in first one, it can be still solved to be written as y = 2 – x2, and its an explicit function. In the second instance, however, we are unable to easily calculate the equation for ‘y,’ and this type of function is referred to as an implicit function, and we will see how to obtain the derivative of an implicit function using the implicit differentiation procedure on this page.
Implicit Differentiation:
The process by which we differentiate implicit function is called as implicit differentiation. A function that can be stated as f(x, y) = 0 is known as an implicit function. i.e., it is difficult to solve for ‘y’ (or) to get into the form of y = f(x). Consider the problem of determining dy/dx given the function xy = 5. Let’s look for dydx using two different process: (a) Solving it for y (b) not solving it for y
Method – a:
xy = 5
y = 5/x
y = 5 x-1
Differentiating both sides with respect to x:
dy/dx = 5(-1 . x-2) = -5/x2
Method – b: 
We turned the implicit function into an explicit function and used the power rule to find the derivative in Method a. However, in method b, we differentiated both sides with respect to x by considering y as a function of x, which is known as implicit differentiation. However, some functions, such as xy + sin (xy) = 0, cannot be written as an explicit function (Method – a). In such instances, the only option to get the derivative is to use implicit differentiation (Method – b).
Implicit Derivative
The implicit derivative is the derivative obtained through the method of implicit differentiation. The implicit derivative of the derivative dy/dx determined in Method-2 (in the preceding example) was originally dy/dx = -y/x. In most cases, an implicit derivative is expressed in terms of both x and y.
Implicit Differentiation and Chain Rule
When determining the derivative of an implicit function, the chain rule of differentiation is crucial. According to the chain rule, d/dx (f(g(x)) = (f’ (g(x)) g’ (x). The chain rule comes into play whenever we encounter the derivative of y terms with respect to x, and we multiply the actual derivative (by derivative formulae) by dy/dx as a result of the chain rule. Here given some of them .
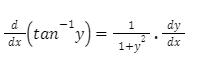
To put it another way, wherever y is differentiated, write dy/dx as well. It’s a good idea to go over these examples again and again because they’re incredibly useful for implicit differentiation.
Process of Implicit Differentiation
Differentiate with respect to x
Collect all the dy/dx
on one side Solve for dy/dx
Example 1: Find dy/dx by implicit differentiation: 3x + 2y = cos y.
Solution:
Given,
3x + 2y = cos y
Differentiating to both sides with the respect to x,
Answer:The implicit derivative, dydx = -3/(2 + sin y).
Example 2: Find the second implicit derivative if x2+y2= 4
Solution:
The given equation is,
x2+y2= 4
Finding first implicit derivative:
Differentiating to both sides with the respect to x,
Finding second implicit derivative:
Differentiating both sides for dy/dx again with respect to x:
d/dx (y’) = d/dx (-x/y) (or)
y” = d/dx (-x/y)
By quotient rule,
y” = [ y d/dx (-x) – (-x) d/dx (y) ] /y2
= [-y + xy’]/y2
Substitute y’ = -x/y,
y” = [-y + x (-x/y) ] / y2
= [-y2 – x2]/y3
Answer:The second implicit derivative is, y” = [-y2 – x2]/y3 .
Conclusion:
You can determine the derivative of y with respect to x using implicit differentiation without having to solve the supplied equation for y. Because we assume that y may be represented as a function of x, the chain rule must be employed anytime the function y is differentiated. The chain rule and implicit differentiation are two approaches for readily differentiating equations that are otherwise complex. Both employ the derivatives principles in somewhat different ways to differentiate the complex equations with minimal effort.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out