Complex numbers make finding the square root of negative integers easier. In the first century, a Greek mathematician named Hero of Alexandria came discovered the concept of complex numbers while attempting to find the square root of a negative integer. However, he merely turned negative to a positive and obtained the numeric root value. Furthermore, in the 16th century, Italian mathematician Gerolamo Cardano discovered the real identity of a complex number while searching for the negative roots of cubic and quadratic polynomial formulas.
Many scientific fields, such as signal processing, electromagnetism, fluid dynamics, quantum physics, and vibration analysis, use complex numbers. We may learn about the definition, vocabulary, visualisation, characteristics, and operations of complex numbers in this section.
What are Complex Numbers
The combination of the real number and the imaginary number makes a complex number. The complex number is denoted by the letter Z and is in the form of x + iy. In the complex number x and y are the real numbers . ‘x’ is the real part of the complex number and represented by Re(z), and ‘y ’ is the imaginary part of the complex number and represented by Im (z). ib is the imaginary number.
Z = a + ib
Examples of complex numbers are: 2+3i , −2−5i , 12+32i , etc.
Power of i
The letter i generally is known as the iota which is used to denote the imaginary component of the complex number. Iota (i) is also useful for finding the square root of negative values. As we know that the value of i2 is -1, therefore we can use that to calculate the value of different powers of i. The necessary condition of a complex number is the value of i² = -1. Let us attempt to comprehend the expanding powers of i.
- I = √-1
- I² = -1
- I³ = i.i² = i(-1) = -i
- I4 = (i²)² = (-1)2 = 1
- I4n = 1
- I4n + 1 = i
- I4n + 2 = -1
Properties of a Complex Number
The characteristics of complex numbers listed below can help you better understand complex numbers and perform various arithmetic operations on them.
Conjugate of a Complex Number:
The conjugate of a complex number is created by taking the same real component of the complex number and changing the imaginary part of the complex number to its additive inverse. The sum and product of two complex numbers are both real numbers, which are known as conjugate complex numbers. The conjugate of a complex number z = a + ib ,and z = a – ib.
Reciprocal of a Complex Number:
The reciprocal of a complex number is useful when dividing a complex number by another complex number. The division of complex numbers is the product of one complex number with the reciprocal of another complex number. The complex number z = x + iy reciprocal is
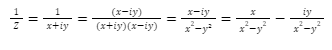
Equality of Complex Numbers:
The complex numbers are equal if the real parts of the complex number and imaginary parts of the complex number are equal. When the real portions of two complex numbers z1=a1+ib1 and z2=a2+ib2 are equal, a1=a2, and the imaginary parts of both complex numbers are equal, b1=b2, they are said to be equal. In the polar form, two complex numbers are identical if and only if their magnitudes are equal and their argument (angle) varies by an integral multiple of 2.
Ordering of Complex Numbers:
It is impossible to organise complex numbers. Unlike real numbers and other similar number systems, complex numbers cannot be sorted. There is no ordering of complex numbers that is consistent with addition and multiplication, thus they do not have the structure of an ordered field. In an ordered field, the non-trivial sum of squares is 0; however, in a complex integer, the non-trivial sum of squares is i2 + 12 = 0. The magnitude of complex numbers, which is their distance from the origin, may be measured and represented in a two-dimensional argrand plane.
How to Solve Complex Function Problems
Addition and Subtraction of a complex number:
To combine two complex numbers, add their real and imaginary components as follows: (a1 + b1i) + (a2 + b2i) = (b1 + b2)i
(12 + 6i) + (11 + 5i) = (12 + 11) + (6 + 5)I = 23 + 11i
(2 – 4i) + (- 6 – 5i) = (2 – 6) + (- 4 – 5)I = – 4 – 9i.
Multiplication of Complex Numbers:
Multiplication of complex numbers differs from multiplication of natural numbers in a few ways. We must utilise the formula i2=1 in this case. The product is z1.z2 = (ca – bd) + i(ad + bc) for the two complex numbers z1 = a + ib , z2 = c + id.
(4 + 5i) – (2 + 3i) = (4 – 2) + (5 – 3)i = 2 + 2i.
Division of Complex Numbers:
The reciprocal of a complex number is used in the division of complex numbers. We have the division as z1 = a + ib, z2 = c + id for the two complex numbers.
Conclusion
Although all real numbers are complex numbers, not all complex numbers must be real.
Although all imaginary numbers are complex numbers, not all complex numbers must be imaginary.
A complex number z=a+ib has the conjugate z=a+ib.
|z|=a²+b² is the magnitude of a complex number z=a+ib.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






