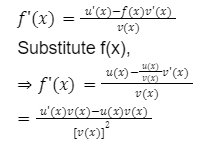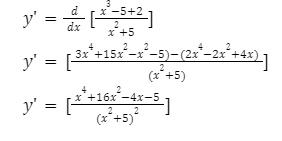Profile
Settings
Refer your friends
Sign out
Determining the type of operator used to connect two functions is an important part of the differentiation process. For example, if a +ve sign is used to indicate a difference between two functions, then those two functions can be distinguished from one another. In contrast, multiplication and division are not able to be done this way. If the functions are dividing, the multiplication rule becomes a little more complicated. Each function is differentiated separately while taking the other function as a constant. Now let’s study the quotient rule, a well-known differentiation rule.
One way to obtain an expression’s derivative or differentiation in calculus is to take the ratio or division of two differentiable functions and divide it by the expression. By this, I mean that while trying to get the derivative of f(x)/g(x), we can use the rule of quotients, because both of these functions are differentiable and g(x) is equal to zero. Products and derivation limitations in differentiation are closely linked to the rule’s application. In the following sections, we’ll go over the formula for the quotient rule and its proof using solved instances. The quotient rule is used to solve the quotient of the functions given if the functions f(x) and g(x) are both differentiable, that is, the derivative of both functions exists.
The Quotient rule states that the derivative of the entire function is the derivative of the numerator times the denominator divided by the square of the denominator.
The quotient rule is simple to remember because the numerator is the same as the product rule’s numerator. Only the square root of the denominator function should be used as the denominator, and the sign should be negative instead of positive.
Apply Quotient Rule in Differentiation :
For the function f(x) = u(x)/v(x) to have a derivative, both u(x) and v(x) must be differentiable functions. Using the quotient rule, we can use the steps below to find the derivation of a function f(x) = u(x)/v(x) that can be changed.
Step 1: Write down what u(x) and v are (x).
Second, Find the values of u'(x) and v'(x), and then use the quotient rule formula:
f'(x) = [u(x)/v(x)]. ‘ = [u(x) – u(x) – v(x)] /[v(x)]²
Let’s look at the example below to get a better idea of how the quotient rule works.
Prove quotient Rule Formula for derivatives :
To prove the quotient rule formula using the implicit differentiation formula, let’s start with a differentiable function f(x) = u(x)/v(x), so u(x) = f(x)v (x). Using the product rule, we get:
Prove quotient rule formula using limit properties :
To show that the quotient rule formula is correct using the definition of limits or derivatives, let the function f(x) = u(x)/v (x).
⇒f'(x)=limh→0[f(x+h)-f(x)]/h
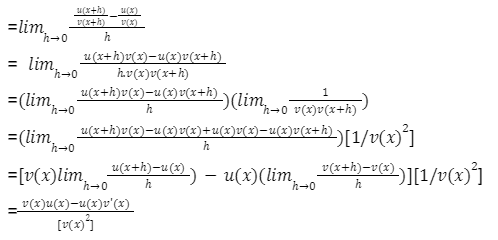
Quotient Rule in limits and derivatives :
When two differentiable functions are divided, the quotient rule in calculus is used to get the derivative of the smaller of the two functions. To put it another way, by subtracting numerator from denominator, divide by denominator’s squared derivative, and divide by squared denominator’s derivative, you get the derivative of a quotient. When given a function of the form: f(x) = u(x)/v(x), the derivative of this function may be found using the quotient rule derivative as follows:
f'(x)=[u(x)/v(x)]’=[v(x)u'(x)-u'(x)v'(x)]/[v(x)]²
Use of Quotient Rule :
Question 1: Differentiate y= x³-x+2 / x²+5
Solution: both numerator and denominator functions are differentiable.
Conclusion :
Determining the type of operator used to connect two functions is an important part of the differentiation process. For example, if a +ve sign is used to indicate a difference between two functions, then those two functions can be distinguished from one another. In contrast, multiplication and division are not able to be done this way.The quotient rule is simple to remember because the numerator is the same as the product rule’s numerator. Only the square root of the denominator function should be used as the denominator, and the sign should be negative instead of positive.When two differentiable functions are divided, the quotient rule in calculus is used to get the derivative of the smaller of the two functions. To put it another way, by subtracting numerator from denominator, divide by denominator’s squared derivative, and divide by squared denominator’s derivative, you get the derivative of a quotient.
