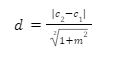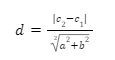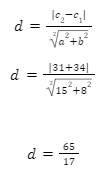How to find the distance between two parallel lines

The distance between two parallel lines simply means how far the two lines are from each other when they are drawn on a plane. A line is a geometric entity that is created by joining a minimum of two points. Many people get confused between the concept of a line and a line segment. A line is a geometric entity that doesn’t have ends, and thus they continue to infinity. While a line segment is a geometric entity that has a specified dimension, and thus it doesn’t reach infinity.

This article will explain the different types of lines, the formula to get the value of the distance between the two parallel lines, and an example question for determining the distance between two parallel lines.

Different types of lines in Geometry

The line is defined as a geometric entity that only possesses length but no width. Moreover, a line can move in both directions. A line consists of an infinite number of points. However, at least two points are required to begin the construction of the line. 

A line in a coordinate system is defined by the equation y = mx +c. Here m is the slope of the line, and c is the intercept. So a point that falls on this line must satisfy the equation of a line. 

A line can be of two types: – 

• Straight line 

• Curved line

Straight lines consist of different lines, and each line is explained below.

• Horizontal lines

A horizontal line is a line parallel to the x-axis in the Cartesian coordinate system. Hence the line doesn’t touch a single point on the x-axis.

• Vertical Lines

Vertical lines are the type of lines that are parallel to the y-axis in a Cartesian coordinate system. Thus the line never intersects with the y-axis in the coordinate system.

• Parallel lines

Parallel lines are the type of lines that run at a certain distance from each other. Thus the parallel lines never meet each other. Parallel lines are generally represented using the || symbol.

• Intersecting lines

The intersecting lines are non-parallel lines that meet each other at a point. An intersecting meet each other at exactly one point, and the point is called the point of intersection.

• Perpendicular Lines

A perpendicular line is a segment that forms a right angle with the other line. In other terms, perpendicular lines are the intersecting lines that intersect each other at 90 degrees.

• Transversal line

A transversal line is a line that intersects two lines that might not be parallel as well. Moreover, a transversal line cuts the two lines at two distinct points in the same plane. 

Distance between two lines

The distance between lines is calculated by taking two reference points on the lines. Generally, the distance between lines is said to be the shortest distance. Distance calculation between two lines is generally done between parallel lines, skew lines, etc. Moreover, the shortest distance between two intersecting lines is zero. Meanwhile, the distance between two skew lines is the perpendicular distance between them.

Steps of the calculating distance between two lines

• The first thing you need to check for finding the distance between the lines is their type. You can check this by referring to the equation of a line.

• If the lines are parallel, then their slopes will be the same. Moreover, if they are perpendicular, then the product of the slopes of the two lines will be equal to -1.

• After this, you need to find the value of intercepts C1 and C2. 

• Then you need to substitute the value of intercept in the equations and find the values of the coordinates.

• After finding all the values, you need to put the values in the distance formula.

The formula for distance between two parallel lines

Consider two lines y = mx + c1 and the other line y = mx + c2. Since the slope of the lines are same, the lines are parallel in nature. Therefore the formula to calculate the distance between such lines is as follows: – 

However, not every line will be represented using the slope-intercept form. If the lines are represented in the ax + by + c1 = 0 and ax + by + c2 = 0 forms then the formula changes to the following: –

Questions on distance between two parallel lines

A line is said to be parallel if the slope between them is equal. Moreover, a set of parallel lines meets each other at infinity.

Question- Find the distance between two parallel line 15x + 8y -34 = 0 and 15x + 8y + 31 = 0

Answer: – 

Equation of first line is: 15x + 8y + 34 = 0

Therefore the values of A, B and C1

Here, A = 15, B = 8 and C1 = -34

Similarly in the second equation the values of A, B and C2 are:

Here A = 15 B = 8 and C2 =31

Now, applying the formula of distance between two parallel lines.

Conclusion

Lines can be defined as a geometrical figure which doesn’t have any thickness. Moreover, the lines extend infinitely in both directions. Therefore, lines are an extremely vital component of geometry. Without lines, shapes such as rectangle, rhombus, square, triangle, hexagon, pentagon, octagon, etc., cannot be produced. 

The formula to calculate the distance between two parallel lines is extremely important. It is one of those concepts that have application in real-life scenarios. For example, a certain distance needs to be maintained while laying the railway tracks. If the concept of parallel lines wasn’t in existence, then laying tracks with uniform distance would have been impossible. Thus the concept of distance between the line is of high importance.