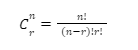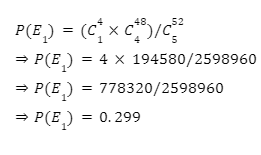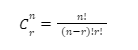How to Calculate the Probability of Combinations

Everything that happens around us is based on a concept called probability. The study of probability allows one to evaluate the happening of an event given an exhaustive list of the parameters that govern that event. It attaches a numerical value to an event that can also help in weighing two events and their viability.

But in various experiments, the selection of things is constantly involved. Selections are usually made from a given set of items. But when such selections are made, the order in which the items are presented does not matter. Then the combinations formula is used to determine all the possible selections.

Combinations Formula

The definition of combinations is a selection of r number of items from a given set of S items in such a manner that the arrangement of the items in the selections does not matter. When selecting k items from a set S—creating a k-combination of a set S—then that k-combination is a subset of the set created by selecting k distinct elements from S. 

The combinations formula is usually quoted as Crn which implies the combinations created by selecting r number of items from a sample set of n elements. In other works of literature, the combinations formula is also given as, rn which is read as “n choose r” and denotes selecting r items from n items. 

In French, Polish, Chinese, Russian and Romanian mathematical literature, the combinations formula is slightly different and given as Cnr which is the same as the traditional formula, the difference being that the number of items to be selected is mentioned as a superscript and the total number of items as a subscript.

The combinations formula for selecting r items from a sample space of n items is equal to

To solve this equation, factorials have to be calculated. A factorial of a number is defined as the product obtained by multiplying the number with all the natural numbers that occur below it. Therefore, n!=n(n-1)(n-2)(n-3)…1

The number of combinations is a binomial coefficient of the expansion;

1+xn=k=0nCknxk

Probability of combinations

May it be a team’s selection or choosing a certain number of balls from a bag, all of these situations involve combinations and, when one of the events is desirable in these experiments, then probability comes into the picture. 

The probability of combinations is calculated by considering all the favourable combinations in the sample set of the experiment and dividing it by all possible combinations possible with the given condition.

The probability of combinations follows all the laws of general probability. The sum of all the probabilities of combinations for a given experiment shall be equal to one. The probability of a combination and that of the combination not occurring complement each other.

Let us consider a sample space of five red balls, ten black balls and four white balls. We are required to find the probability of picking four balls such that two balls are red and the other two are black. 

We start by finding the total number of possible combinations. There are a total of 19 balls in the bag, irrespective of their colour. All the possible combinations of picking four balls from these 19 balls is given as C419. 

Now we need to pick three balls such that one of them is red and two are black. This means that we are picking two red balls from the five red balls and two black balls from the ten black balls. The total combinations of picking two red balls from five red balls are:

C25 

And the total combinations of picking two black balls from the ten black balls are:

C210

Since picking the red ball and the black ball happen simultaneously, the total combinations of picking four balls, in which two balls are red and two balls are black are:

C25C210

Now we calculate the probability of the given situation happening with the sample space of 19 balls.

P =(C25C210)/C419  

Calculating this we get;

P=1045/3876

P=0.116

Probability of combinations questions

Q. Consider a deck of 52 playing cards. What is the probability that one of them will be an ace upon picking five cards at random from this deck?

Ans

Let us define an event

E1: Event that five cards are picked at random from the deck, one of them is an ace.

First, we start with finding all the possible combinations of picking five cards at random from a deck of 52 cards.

The number of combinations can be given as; C552. 

Therefore, the total of possible combinations is C552.

Now, we need to find the total possible combinations favourable to E1. For a combination to be favourable to E1, it needs to have one ace in it. There are four aces in a deck, and selecting one ace from four aces can be done in C14 ways. The remaining four cards can be any card but not an ace. 

Therefore, from all the 48 remaining cards, four cards need be selected after removing the four aces, which can be done in C348.

Hence, the total number of combinations that are favourable to E1 can be given as:

C14C448.

The probability of event E1 happening can now be calculated as:

Conclusion

The definition of combinations is a selection of r number of items from a given set of S items in such a manner that the arrangement of the items in the selections does not matter. 

When selecting k items from a set S, that is creating a k-combination of a set S, then that k-combination is a subset of the set created by selecting k distinct elements from S. 

The probability of combinations is calculated by considering all the favourable combinations in the sample set of the experiment and dividing it by all possible combinations that are possible with the given condition.