According to Nikolai Luzin, a Russian mathematician who lived from 1883 to 1950, “Rolle’s theorem underpins the theoretical evolution of differential and integral calculus.” Rolle’s theorem is widely used in physics, astronomy, and other sciences. Rolle’s Theorem in action: When you throw a ball vertically up, its initial displacement is zero (f (a)=0), and when you catch it again, it’s zero (f (b)=0). And differential and integral calculus are unquestionably important in a variety of sectors in our daily lives; a few examples are as follows:
1) Rolle’s theorem is extremely useful in determining the projectile trajectory’s maximum height.
2) It was instrumental in achieving architectural excellence in the construction of elliptical domes, which increases the amplitude of light (electromagnetic) and sound waves.
3) A few weeks ago, I had the opportunity to use Rolle’s theorem to determine which day in a certain interval has the same amount of registered COVID-19 cases.
Analysis
Let’s try to approach Rolle’s Theorem by following this easy example. We would expect the speedometer reading to be exactly 50 miles per hour at least once throughout the trip if a car travels smoothly down a straight level road at an average speed of 50 miles per hour. After all, if the car’s speed was always above 50 miles per hour, the average speed would be higher, and vice versa if the speed was always below 50 miles per hour. If s(t) represents the car’s position at a time ‘to during a trip across the time interval a to b, then t = c is the time when the velocity s'(c) equals the average velocity between times t=a & t=b. That is, in some cases. In other words, given some c with a<c<b,
(s ( b) − s ( a) )/(b – a) = s′( c)
Where the right-hand expression represents instantaneous velocity and the left-hand expression represents the average velocity.
Application of Rolle’s Theorem in Real Life
There are various examples that can help us grasp how Rolle’s theorem helps us handle a variety of real-world jobs; I’ve tried to assemble a few below.
A few days ago, I was looking at government statistics on COVID-19 delta cases published by the “Centers for Disease Control and Prevention” in the United States, and the graph of days vs. new cases looked something like this.

I noticed that the number of cases registered on June 1st and July 10th was the same, and that the graph is nicely continuous and differentiable both within and beyond the interval;

Let’s say a=June 1st and b=July 10th, and the graph’s curve represents a specific function f(x), and we want to discover a specific day ‘c’ inside the interval [a,b] where the number of recorded cases remains constant.
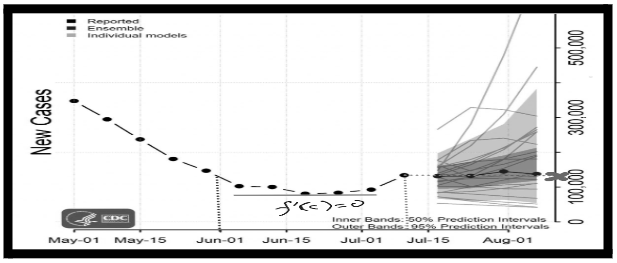
i.e. no change has been observed, then Rolle’s theorem will undoubtedly play its part, and through
f'(c) =0
That day will be found.
2) Rolle’s theorem is also very useful in determining the maximum height of a projectile trajectory. Consider the following example:
The equation for a projectile’s trajectory is y=10x-(9/5) x 2 (m). What position will you be in when the maximum height is reached?
Now, the first thing I’ll do is find the interval [a, b] such that f(a) = f(b), where the lower bound ‘a’ is the projectile’s “launching point” and the higher bound ‘b’ is the projectile’s “landing point.” Examine the projectile trajectory graph.

Theorem of Rolle in Projectile Motion
Here, y = f(x), the launching and landing points are the trajectory’s x-intercepts, which can be calculated by equating f(x) =0, i.e.
Thus,
x=0 and x=18
To identify the position of the maximum height, we must trace its stationary point (extrema), which is, of course, “maxima,” a point where the tangent’s slope is zero.

We can see that the above curve is continuous with [0,18] and differentiable within]0, 18[, implying that there is a point ‘c’ ]0, 18[where f'(c) =0, and that this ‘c’ is the spot where the projectile reaches its greatest height.
By dividing the above equation by c, we get:
y=f(9)
=10(9) − (5/9) (9)2
=90−45
=45m
i.e., the projectile will reach a maximum height of at c=9m.

3) What about using Rolle’s work in dome construction?
Despite the fact that our mediaeval Muslim civilisation was older and richer than this French Mathematician’s work, this French cheese made a significant contribution to making architectural calculations easier by easily transitioning from 2D to 3D.
Take a look at the “Sultan Ahmed Masjid,” also known as the “Blue Mosque,” Istanbul’s final imperial masjid, which was built between 1609 and 1617 and is a testament to the Ottomans’ architectural prowess.
Domes are created not only to improve the beauty of any structure, but also to maintain a decent sound echo. The heights of the domes play an important part in amplifying sound waves and turning them in the right direction so that everyone can hear properly.
We can simply establish the maximum height of domes and arches using this French theorem, preserving the monuments’ stability and architectural beauty.
Conclusion
The study of algebraic equations has resulted in two fundamental statements in the theory of functions:
The root interval theorem
A derivative’s root theorem
The result was the Mean Value Theorem.
Several authors refer to the “Theorem of root interval” as “Second Rolle’s Theorem” or “Theorem of Bolzano Cauchy” in Russian literature.
It took roughly 300 years for Rolle’s Theorem to reach its ultimate form. It has a huge impact on differential geometry, functional analysis, mechanics, and other fields.
“Theoretical evolution of differential and integral calculus is based on this theorem.”
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






