Heron’s Formula

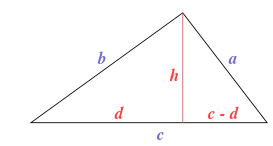
Using Pythagoras Theorem,

            b2=d2+h2

            This is the 1st equation

              Also:-

           a2=h2+(c-d) 2

           This is the 2nd equation

           From 1st equation, 

           h2=b2-d2

           This is the 3rd equation 

           Substituting this value in the second equation,

           a2=b2-d2+(c-d) 2

           a2=b2-d2+c2-2cd+d2

           a2=b2+c2-2cd

           a2-b2=c2-2cd

           No we have to solve for d

           2cd=c2-a2+b2

           d= (-a2+b2+c2)/ (2c)

           Substituting this value in the 3rd equation,

           h2=b2-d2

           h2=b2-((-a2+b2+c2)/ (2c)) 2

           Now we have to apply the difference of squares identity here which states:-

           a2-b2= (a+b)*(a-b)

           So,

           h2= ((b+ ((-a2+b2+c2)/ (2c)))*(b-((-a2+b2+c2)/ (2c))))

           h2= ((2bc- a2+b2+c2)/ (2c))*((2bc+a2-b2-c2)/ (2c))

           h2= ((2bc- a2+b2+c2)*(2bc+a2-b2-c2))/ (4c2)

           We know that b2+c2+2bc= (b+c) 2 and b2+c2-2bc= (b-c) 2

           So using those,

           h2= (((b+c) 2-a2)*(a2-(b-c) 2))/ (4c2)

           h2= ((b+c-a)*(b+c+a)*(a+b-c)*(a-b+c))/ (4c2)

           Now since we know that,

           s= (a+b+c)/2

           So,

           (a+b+c)=2s

           h2= ((b+c-a)*2s*(a+b-c)*(a-b+c))/ (4c2)

           h2= ((2s-2a)*2s*(2s-2c)*(2s-2b))/ (4c2)

           h2= (2*(s-a)*2s*2*(s-c)*2*(s-b))/ (4c2)

           h2= (4*s(s-a)(s-b)(s-c))/(c2)

           Now as we can see in the above figure,   

            Area=(c*h)/2

            So substituting the value of h in the Area equation,

            A=√((c2/4)*((4s(s-a)(s-b)(s-c))/(c2)))

            A=√(s(s-a)(s-b)(s-c))

            Hence Proved

Heron’s Formula for Equilateral Triangle

            A=√(s(s-a) (s-b) (s-c))

            Since all three sides are equal a=b=c

            A=√(s(s-a) (s-a) (s-a))

            Substituting the value of s= ((a+b+c)/2)

            A=√((3a/2)((3a/2)-a) ((3a/2)-a) ((3a/2)-a)))

            A=√((3a/2)*((3a/2)-a)3))

            A=√((3a/2)*((a/2)3))

            A=√((3a4/16))

            A=(√3)*((a2)/4)

            A=(√3/4)*(a2)

Heron’s Formula for Isosceles Triangle

So let’s assume that sides a and b of a triangle are equal,

                 a=c

Now we can use that in the heron’s formula,

             A=√(s(s-a)(s-b)(s-c))

            A=√(s(s-a) (s-a) (s-b))

            This is the 1st equation             

             s= (a+b+a)/2

             s= (2a+b)/2

             s=a+ (b/2)

            Substituting this in the 1st equation

            A=√(s(s-a) (s-a) (s-b))

            A=√((a+(b/2))((a+(b/2))-a) ((a+(b/2))-a) ((a+(b/2))-b))

            A=√((a+(b/2))(b/2)(b/2) ((a+(b/2))-b))

            A=√((a2-(b/2)2)*(b/2)2)

            A=√(((a2b2)/4)-(b4/16))

            A=(b/4) √(4a2- b2)

Examples

Below are solved few examples involving Heron’s formula-

Q. Find the area of an isosceles triangle by Heron’s Formula. The lengths of the triangle are given as 7,7,10.

Soln. 

Using the formula for Isosceles triangle:-

A= (b/4) √ (4a2- b2)

A= (10/4) √ ((4*49)-100))

A=24.495

Q. Find the area of an equilateral triangle with the length of a side given to be 9.

Soln.

Using the formula for an equilateral triangle:-

               A= (√3/4)*(a2)

               A= (√3/4)*(92)

               A=35.074

Q. Find the area of a triangle with the lengths of the sides given as 7,8 and 9.

Soln.

A=√(s(s-a)(s-b)(s-c))

 s=(a+b+c)/2

s=34/2=17

A=√(17*10*9*8)

A=110.634

Conclusion

In this article, first, we saw a brief history of The Heron’s Formula. Then we saw the actual representation of the formula. We also noted that this formula is very useful since we need not know the angles of the triangle to find out the Area of the Triangle.

Then we moved on to the introduction Part. In the introduction, first, we saw the complete proof of The Heron’s Formula using the Pythagorean Theorem. Then we devised Heron’s Formula for Isosceles and Equilateral Triangles. After that, we solved some problems which made use of this theorem.