Heights and Distances

One of the important applications of trigonometry is height and distance. In architecture and astronomy, it has very useful and important applications such as calculating distances, slopes, etc. The concept of height and distance is used in our everyday life. It deals with studying the relationship between the sides of the triangle and its angles. The mathematical calculation for this can be done by using trigonometry. In this article, we will learn about this important application of trigonometry and understand the basic concept of height and distance.

What are heights and distances?

The measurement of an object vertically is known as height, and the measurement of an object horizontally is the distance of an object from the point. To understand this concept in detail, we need to understand the definition of height and distance. 

Line of sight 

It is an imaginary line drawn from the observer’s eye to the point seen by the observer.

Angle of elevation

When the observer has a line of sight above the horizontal, the angle from the horizontal upward of an object is called the angle of elevation. For example, let point C be the point at which the observer is looking above the horizontal line. The CO represents the line of sight. Thus the angle of elevation is represented by angle COA.

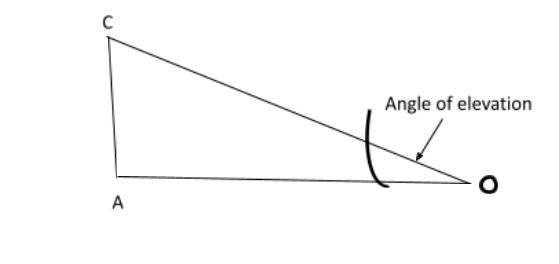
Angle of depression

When the observer has a line of sight below the horizontal line, the angle from the horizontal upward is called the angle of depression. For example, let B be the position of the object at which the observer is looking. Thus the angle of depression is represented by angle ABO.

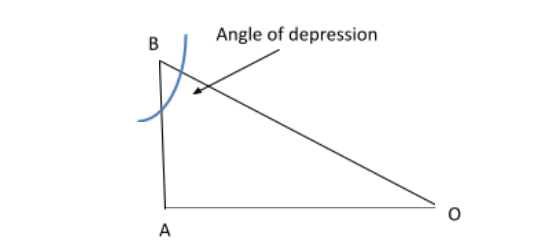
Using these definitions, we can easily find the distance and height with the help of some formulas.

Height and Distance Formula

By using the trigonometry ratio, we can easily find distance and height. These trigonometric ratios can be used in right-angle triangles. The right-angle triangle has a perpendicular side, a base and a hypotenuse. As we know, heights are measured vertically, and distances are measured horizontally; thus, in these right-angle triangles, the perpendicular side represents the height. The horizontal side, which is the base of the right-angled triangle, represents the distance of an object from a point.

Let us discuss some cases that we encounter while solving the problems on heights and distances.

(a) In ∆ABC, right angles at B, ‘h’ represents the height and ‘d’ represents the distance.

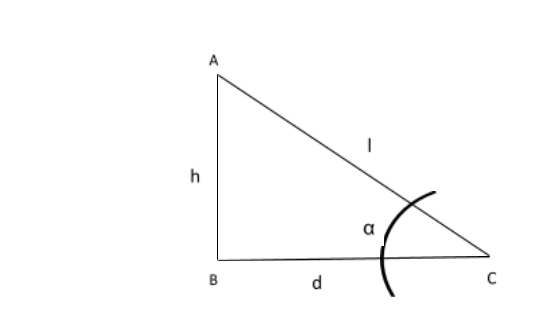
Sin = hl

Cos = dl

tan = hd

The height and can easily be calculated using h = d x tan

(B) In In ∆ABC, if DE || AB, then

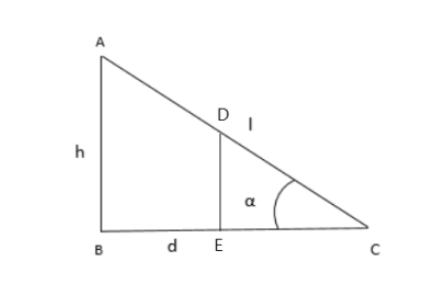
ABDE= BCEC

(C) In ∆ABC, PC = x and the value of x is,

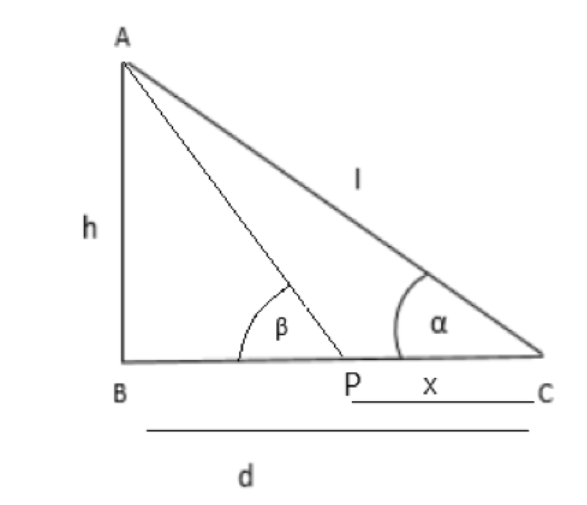
 x = h (cotα – cotβ)

From the above three cases, we can easily calculate the height and the distance by using these formulas according to the conditions given in the problem.

We can use trigonometric ratio tables to calculate the value of sinα, cosα, tanα etc.

Solved examples 

• Calculate the height of the object if the observer is standing 5m away from the object with an angle of elevation of 60°.

Solution.

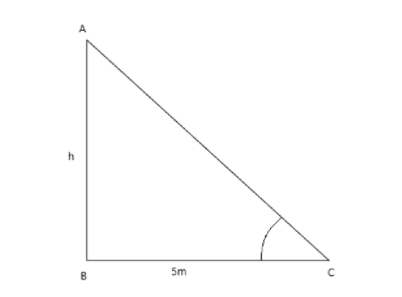
Let h be the height of the object, such that 

tan = hd

the angle of elevation is given 60° and d = 5m, hence 

tan60 = h5

h = 5 x tan60

Since tan60 =√3

h = 5√3m

2. A man is standing at the bank of the river, looking at the top of the tower with an angle of elevation 45°. He moves 30m away from the bank, and now the angle of elevation becomes 30°. Calculate the height of the tower at which he is looking.

Solution.

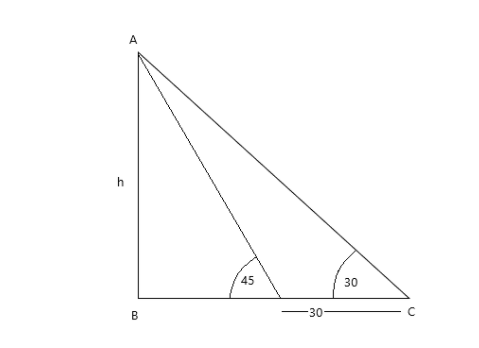
As we know, x = h (cotα – cotβ)

Here a mon moves 30m away from the tower, thus x = 30 and α = 30 and β = 45 

Now, 30 = h(cot30 – cot45)

30 = h(3-1)

•   h = 303-1)

h = 303-1) x (3+1) (3+1)

h = (303+1) (3-1)

h = 15(3-1)m 

Conclusion

In this article, we have learnt about heights and distance, which are some of the important applications of trigonometry. The concept is used in our daily lives. Also, it is very useful in astronomy and biological studies. The heights and distance can be understood with the help of some terms like the line of sight, angle of elevation and angle of depression. The angle between the observer’s line of sight and above the horizontal is the angle of elevation, and the angle between the observer’s sight and below the horizontal is known as the angle of depression. Heights and Distances can be calculated by using trigonometric concepts.