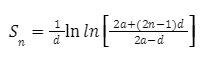Harmonic Progressions and Series

A harmonic progression is a mathematical progression that is created by taking the reciprocals of an arithmetic progression. When each term is the harmonic mean of the neighboring terms, a sequence is equivalently a harmonic progression. The Euler–Mascheroni constant is the infinite series formed by adding all positive unit fractions: is the harmonic series. The harmonic series has no finite limit because the logarithm has arbitrarily large values: it is a divergent series.

Harmonic Progression Definition

“When the reciprocals of elements are in arithmetic progression, a series of terms is called a Harmonic progression series”.

If p, q, r, and s are in arithmetic progression, then 1/p, 1/q, 1/r, and 1/s are all in harmonic progression.

For example:

1/10, 1/12, 1/14, and 1/16 are the first four numbers in the series. . . . . . . . 10, 12, 14, 16 are the reciprocals of the given series. . . . . . . The first term is ’10,‘ and the common difference is ‘2.’ The series is clearly in Arithmetic progression.

As a result, the given series is progressing in a Harmonic manner.

Harmonic Progression Formula

To solve harmonic progression problems, we must first determine the arithmetic progression sum. It means that the reciprocal of the nth term of the corresponding A.P. is equal to the nth term of the harmonic progression. As a result, the formula for determining the nth term of the harmonic progression series is:

T _n of the (H.P) is=1 / a+(n-1)d

Where,

A.P.’s first term is “a.”

A common difference is “d.”

The number of terms in A.P. is “n.”

The formula above can also be written:

n^th term of H.P=1 / (n ^th term of the corresponding A.P)

Harmonic Progression Sum

If the harmonic progression is 1 / a,1 / a+d,1 / a+2d…….1 / a+(n-1)d, the formula to find the sum of n terms in the harmonic progression is:

The sum of the n^th terms

Where,

“a” = A.P’s first term,

“d” = A.P’s common difference,

“ln” = the natural logarithm

Harmonic Progression Examples

Problem: 1 If the fifth term is 1/16 and the eighth term is 1/25, find the harmonic progression’s 12th term.

Solution: Given, the fifth term = 1 / a+4d = 1 / 16

And the eight term = 1 / (a+7d) = 1 / 25

When we compare these, we get a + 4d = 16 and  a + 7d = 25.

We get a = 4 and d = 3 by solving these two expressions.

Harmonic progressions 12^th term =1 / (a+11d) = 1 / (4+11×3) = 1 / (4+33) = 1 / 37

As a result, the harmonic progressions 12^th term is1 /37.

Conclusion

In this article we conclude that, in harmonic progression, any term in the sequence is considered the harmonic mean of its two consecutive terms. The reciprocals of an arithmetic progression that does not contain 0 are used to find real numbers in a harmonic progression. This article explains harmonic progression in detail, including formulas and solutions. Harmonic progression has a variety of uses in our everyday lives. Understanding how water boils when the temperature changes by the same value is easier with harmonic progression. It’s also used to count the number of raindrops that fall.