A harmonic progression (H.P.) is a mathematical progression that is created by taking the reciprocals of an arithmetic progression. When each term is the harmonic mean of the neighboring terms, the series is a harmonic progression
A harmonic progression of separate unit fractions cannot add to an integer (unless in the simple situation where( a = 1 and d = 0). The reason for this is that the progression will have at least one denominator divisible by a prime number that does not divide any other denominator.
Harmonic progression Sum
Arithmetic Progression (AP): An arithmetic progression (AP) or arithmetic sequence is a set of numbers in which the difference between successive terms is constant.
Harmonic progression: A harmonic progression (or harmonic sequence) is a progression created by multiplying the reciprocals of an arithmetic progression.
This harmonic progression must now be created. Even the sum of the created sequence must be calculated.
- It is straightforward to generate HP or 1/AP. In an AP, a + (n-1)d is the nthterm. We can quickly create the sequence using this formula.
- Compiling the sum of this progression or sequence can be tedious. We may either iterate while creating this sequence or utilize approximations to create a formula that will give us a value that is accurate to a few decimal places.
Sum = 1/d (ln(2a + (2n – 1)d)
Theorem
If and only if, the terms of a series are the reciprocals of an arithmetic progression that does not contain 0. it is a harmonic progression.
Proof
The mean harmonic of 1/a+n-1d and 1/a+n+1d
2/a+n-1d+a+n-1d=2/2a+2nd=1/a+nd’
This proves the statement’s “if” component. The portion about “only if” is similar and is left as an exercise: write the first two phrases as 1/a and 1/a+d and how the third term works 1/a+2d The fourth and final term is 1/a+3d via induction, and so on.
Sum of n terms in the harmonic progression
A harmonic progression’s partial sums are frequently of interest. The harmonic numbers, for example, are partial sums of the harmonic progression 1,1/2,1/3……
The purpose is to calculate the sum of the terms Sn, 1/a,1/a+d,….1/a+n-1d where d>0
Take the F function as an example fx=1x Start with Riemann sums with rectangles of width d.
x=a to x=a+n-1d
The length of the ith rectangle is 1 / a+i-1d’, while the width of each rectangle is d. As a result, the area under the curve will be about equal to the sum of the areas of these rectangles.
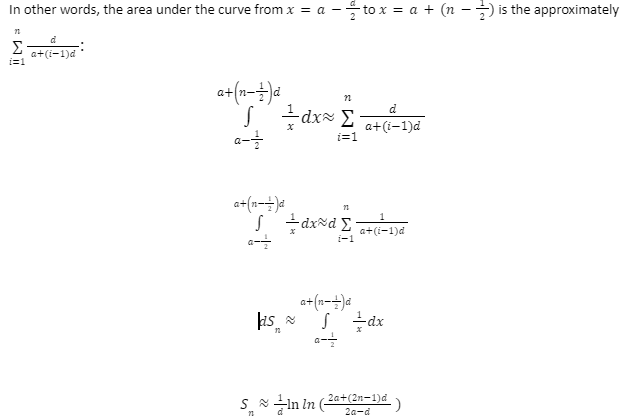
where 2a ≠ d and d ≠ 0
When n is quite large compared to d, this formula provides a good approximation.
Problems on Harmonic Progression
Problem: 1 Find the fourth and eighth terms from the series 6, 4, 3,…
Solution: We can convert this H.P. to an A.P. using reciprocal.
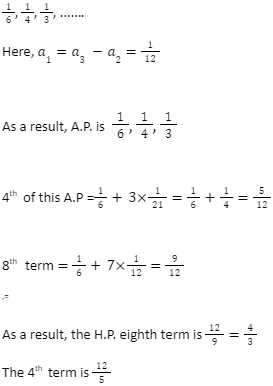
Problem: 2 What is the value of the harmonic progression’s 21st and nth terms: 1/5, 1/9, 1/13, 1/14…..?
Solution: The harmonic sequence is 1/5, 1/9, 1/13, 1/14…
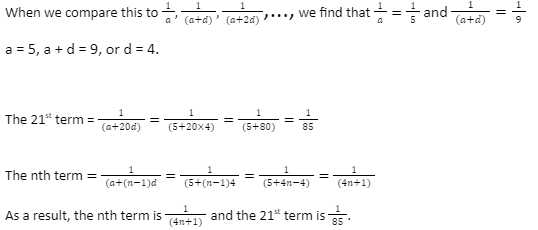
Conclusion
We conclude that in mathematics, the harmonic sequence can be defined as the reciprocal of the arithmetic sequence with values other than 0. Harmonic series is the accumulation of harmonic sequences. It’s an unending sequence with no end.To solve the harmonic progression problems, we must find the appropriate arithmetic progression sum. The reciprocal of the nth term of the associated A.P. equals the nth term of the harmonic progression. As a result, the formula for calculating the harmonic progression’s nth term has been developed.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out



