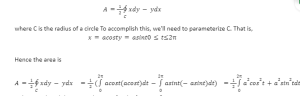Green’s theorem is primarily used for the integration of a line and a curved plane. The relationship between a line integral and a surface integral is demonstrated by this theorem. It is related to many theorems, including the Gauss theorem and the Stokes theorem.
It is named after George Green, who published a similar finding in his 1828 publication An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism. Augustin-Louis Cauchy published a paper in 1846 that included Green’s theorem in the penultimate sentence. In reality, this is the first printed statement of Green’s theorem in the form used in modern textbooks. In his PhD dissertation on the theory of functions of a complex variable, Bernhard Riemann provided the first demonstration of Green’s theorem.
What exactly is Green’s Theorem?
Green’s theorem is one of calculus’ four fundamental theorems, all of which are inextricably linked. You will understand how Stokes theorem is based on the principle of linking the macroscopic and microscopic circulations once you understand the concept of the line integral and surface integral. Green’s theorem, on the other hand, defines the relationship between the macroscopic circulation of curve C and the sum of the microscopic circulation that is contained within the curve.
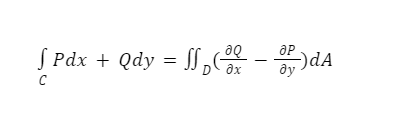
In other words, Green’s theorem establishes a link between a two-dimensional vector field’s line integral over a closed path in the plane and the double integral over the region it encloses.
Statement of Green’s Theorem
Let C denote a positively oriented, smooth, and simple closed curve in a plane, and D denote the region bounded by C. If L and M are continuous partial derivatives of functions of (x, y) defined on the open region containing D, then Green’s theorem is expressed as
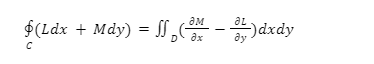
Where the path integral is traversed counterclockwise in conjunction with C.
Area of Green’s Theorem
The area of the closed curves can be calculated using Green’s theorem.
According to Green’s theorem,

Applications of Green’s Theorem
Green’s Theorem is a subset of Stokes Theorem in which the surface is completely in the plane. However, in simpler versions. Especially in the case of a vector field in the plane. It is also used to compute area; the tangent vector to the boundary is rotated 90° clockwise to create the outward-pointing normal vector in order to deduce Green’s Theorem’s divergence form.
There are numerous other uses of Green’s Theorem that we cannot expect to cover in this effort. Green hoped that scientists would use calculus to advance our understanding of electricity and magnetism, and he proposed some fundamental ideas for how this could be accomplished, including the idea that we may understand properties inside an object by observing its outside.
Cauchy and Riemann, among others, wrote extensively about Green’s ideas, as we’ve seen. They formalized his theorem and eventually applied it to the domain of complex numbers (which themselves have important applications in electronics). However, as we read Green’s Essay, It is obvious that Green recognized the potential of his concepts to alter our knowledge of a wide range of phenomena.
An overview of Green’s Idea
Despite Green’s complaint that the windmill “provided few possibilities for mental progress,” scientists currently employ Green’s Theorem (along with related notions like Stokes’ Theorem, the Divergence Theorem, and so on) to better analyze and create renewable energy sources like wind power. Furthermore, the idea that we can measure the border of a closed surface and utilize this to learn about the inside of the surface has had a significant impact on our knowledge of many physical processes.
Green’s concepts appear in more areas as we discover more about our Universe. Donald Marloff, a theoretical physicist, is one person who believes the Universe may have a boundary. If true, “quantities that one would imagine are a priori independent are in fact linked together,” writes Marloff. As a result, boundary observables can be identically equal to bulk observables.” In other words, if space has a boundary, physical processes on that boundary are similar to those occurring within the Universe itself. An observer looking only at the boundary would have complete knowledge of the bulk, or interior, of our Universe. One conclusion is that the entire Universe may be squashed onto the volume, rendering it obsolete. While we believe we live in the centre of the Universe, it is possible that this is an illusion and that we all exist at a lower dimension on a border.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out