One of the most important ideas in algebra is graphing linear equations. A linear equation is a one-dimensional equation, which means that the exponents of variables in a linear equation may only be 1 and cannot be more than 1 in any scenario. Linear equations can include one or more variables. The graphical approach is one of the ways for solving linear equations, either one or two variables linear equations, and it is one of the methods for solving linear equations.
What Is Linear Equations?
A linear equation is an equation of a maximum degree of 1, i.e. no variable has an exponent larger than 1. A linear equation’s graph is a straight line, always. A linear equation is an algebraic equation in which each term has an exponent of 1 and which, when graphed, always produces a straight line. This is why it is referred to as a ‘linear equation.’ There are one-variable linear equations and two-variable linear equations
Example: y=6x+4
Ax + B = 0 is the conventional or general form of linear equations in one variable, where A and B are real values and x is the single variable. Ax + By = C is the conventional form of a two-variable linear equation, where A, B, and C are any real numbers, and x and y are the variables.
Graphing Linear Equations
Solving linear equations and representing the solution on a coordinate plane is what graphing a linear equation is all about.
A vertical line parallel to the y-axis forms the graph of a linear equation with one variable x, and vice versa, whereas a straight line forms the graph of a linear equation that has two variables x and y.
Let’s use the following example to graph a linear equation with two variables.
Plot a graph for the linear equation x – 2y = 2 in two variables.
Let’s make a plot of the linear equation graph using the procedures below.
Step 1: x – 2y = 2 is the given linear equation.
Step 2: Substitute y = mx + b into the equation. As a result, y = x/2 – 1 will be obtained.
Step 3: To build the coordinates, we can now swap the value of x with different integers and retrieve the corresponding value of y.
Step 4: Putting x = 0 in the equation gives us y = 0/2 – 1, or y = -1. In the same way, if we replace x with 2 in the equation, y = x/2 – 1, we get y = 0.
Step 5: Substituting 4 for the value of x gives us y = 1. When x = -2, the value of y = -2 is obtained. Now, the supplied linear equation y = x/2 – 1 is satisfied by these pairs of (x, y) values.
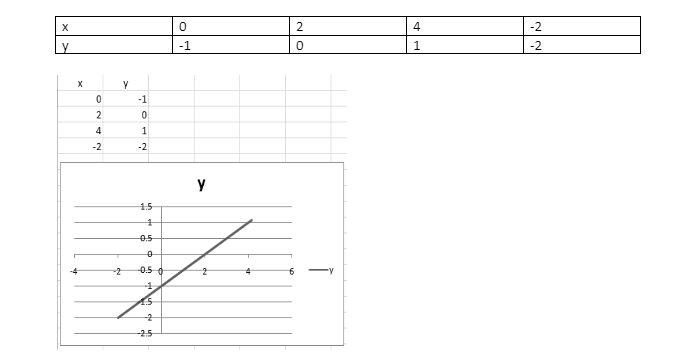
Step 6: Finally, we plot the points (4,1), (2,0), (0,-1) and (-2, -2) on a graph and connect them to form a straight line. On a graph, this is how a linear equation is represented.
Example: Draw a graph of the linear equation x+2y=7.
Solution:
The following are the steps we’ll take:
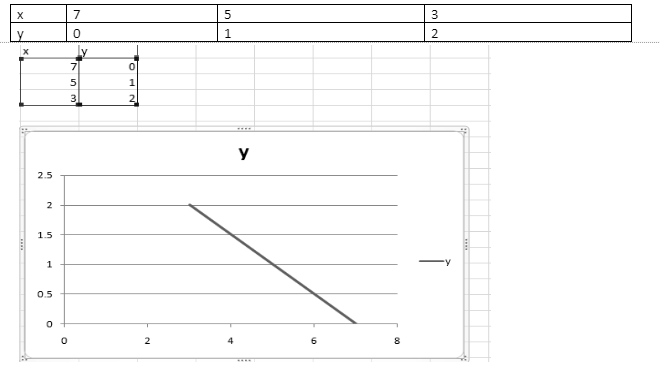
Step 1: Determine whether the provided linear equation x+2y=7 is written in the form y = mx + b. [We get y = – (1/2) x + 7/2 when we convert.]
Step 2: Determine the x and y-intercepts. Put y = 0 in the following equation: x = 7-2(0), x=7. Put x=0 in the equation now. y=7/2 = 3.5, 2y=7-(0)
Step 3: Using trial and error, identify three pairings of (x, y) values that fulfill the provided linear equation x=7-2y. (Please see the table below.)
Step 4: Draw a graph with the points (7,0), (5,1), and (3,2) on it.
Step 5: Make a straight line by connecting all of the points shown on the graph paper.
Linear Equations In One Variable
A linear equation in one variable is an equation with only one variable. It takes the shape Ax + B = 0, with A and B being any two real numbers and x being a single-valued unknown variable. It’s the most straightforward way to convey a mathematical statement. The degree of this equation is all the time equal to one. A one-variable linear equation is moderately simple to solve. To find the value of the unknown variable, the variables are split and brought to one side of the equation, while the constants are combined and brought to the other side.
Example: Solve the linear equation 3x + 6 = 18 in one variable.
We bring the numbers to the right-hand side of the equation and keep the variable on the left-hand side to solve the given equation. This translates to 3x = 18 – 6. Then we obtain 3x = 12 when we solve for x. Finally, x = 12/3 = 4 is the value.
Linear Equations In Two Variable
Ax + By + C = 0 is a two-variable linear equation in which A, B, and C are real integers, and x and y are the two variables, each with a degree of 1. Simultaneous linear equations are two linear equations that have the same solution. 6x + 2y + 9 = 0 is a two-variable linear equation, for example. The graphical approach, substitution method, cross multiplication method, elimination method, and determinant method are all methods for solving linear equations in two variables.
How To Solve Linear Equations?
A weighing balance with equal weights on both sides is an equation. It still holds true if we add or subtract the same amount from both sides of an equation. It is also correct to multiply or divide the same number into both sides of an equation. We find the value of the unknown variable by bringing the variables to one side of the equation and the constant to the other. This is how you solve a one-variable linear equation. Let’s look at an example to help us comprehend.
Solve the equation 3x – 2 = 4 as an example.
So that the balance is not disturbed, we do mathematical operations on the Left-hand side (LHS) and the right-hand side (RHS). So, add 2 on both sides to reduce the LHS to 3x. This will not upset the equilibrium. 3x – 2 + 2 = 3x and 4 + 2 = 6 are the new LHS and RHS, respectively. Let’s decompose the LHS to x by dividing both sides by three. As a result, we obtain x = 2. This is one of the methods for solving one-variable linear equations.
Linear Equation Hints:
- The solution or root of a linear equation is the value of the variable that makes the equation true.
- When the same number is added, subtracted, multiplied, or divided into both sides of a linear equation, the solution remains unchanged.
- A linear equation with one or two variables always has a straight line as its graph.
Conclusion
This article has sufficiently provided information regarding the graphing of linear equations. Linear equations in one variable as well as in two variables can be solved graphically using the steps mentioned in the article.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






