Profile
Settings
Refer your friends
Sign out
We graph inequalities like we graph equations but with an additional step of shading one facet of the line.
Graphing Linear Inequalities
Firstly, draw the “equals” lines, then shade them to identify
When solving a system of linear inequalities graphically we will follow these steps:
Solve the inequality for y.
Treat the inequality as a linear equation and graph the line as either a solid line or a
Dashed line depending on the inequality sign.
If the inequality sign does not contain an equal sign (< or >) then a dashed line is drawn.
If the inequality sign has ≤ or ≥, then draw the line as a solid line.
Shade the region satisfying the inequality
Do steps from 1 – 3 for each inequality
The solution set will be the overlapped region of all the inequalities.
Example 1: Graph the linear inequality y > 2x – 1.
The primary aspect is to make sure that variable y is by means of itself at the left side of the inequality symbol, which is the case in this trouble.
y>2x-1 ( greater than symbol)
y=2x-1( equal symbol)
Graph the road y > 2x – 1 inside the xy axis the usage of your chosen approach. Because the inequality image is simply more than “>”, and now not more than or identical to “≥“, the boundary line is dotted or dashed. So here’s the way it has to look up to now.
The remaining step is to shade either above or below the boundary line. From the recommended steps, we have been instructed to shade the top side of the boundary line if we’ve the inequality symbols > (more than) or ≥ (more than or identical to). Usually keep in mind that “extra than” implies “top”.
Affirm if our graph is correct by picking the point (4,2) within the shaded phase, and compare the values of x and y of the point inside the given linear inequality.
From the selected test points, x=4 and y=2
We have the right statement which makes us able that our final graph of the inequality is correct as well.
Graphing Inequalities In Two Variables
To graph, a linear inequality in two variables (say, x and y ), first get y on one facet. Then remember the related equation received by changing the inequality sign to an equals signal. The graph of this equation is a line.
If the given inequality is drawn, ( < or > ), graph a dashed line. If the inequality isn’t always strict ( ≤ and ≥ ), graph a solid line.
Then pick one point no longer on the road ( (0,0) is typically the perfect) and decide whether those coordinates fulfill the inequality or not. If they do, shade the half-plane containing that point. In the event that they don’t, shade the alternative half-plane.
Example -: Graph the inequality y ≤ 4x−2 .
This line is already in slope-intercept form , with y alone at the left facet. Its slope is 4 and its y -intercept is −2 . So it’s straightforward to graph it. In this example, we make a solid line because we have a “less than or identical to” inequality.
Now, putting x=0,y=0 to decide whether or not (0,0) satisfies the inequality.
0≤4(0)−2
0≤−2
That is false. So, shade the half-plane which does now not consist of the point (0,0) .
Graphing Inequalities on a number line
We also can graph inequalities on the number line. The subsequent graph represents the inequality x≤2.1/2 The dark line represents all the numbers that fulfill x≤2.1/2. If we pick any variety on the darkish line and plug it in for x, the inequality may be true.
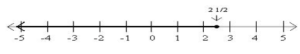
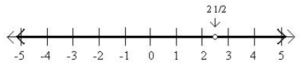
Graph of the Inequality x≠2.1/2
An inequality with a “≠” sign has a solution set that is all the actual numbers besides a single factor (or some of single points). Therefore, to graph an inequality with a “≠” sign, graph the whole line with one factor eliminated. As an example, the graph of x≠2.1/2 seems like:
Graph of the Inequality x≠2.1/2
Conclusion
Graphing inequality, cope with the <, ≤, >, or ≥ signal as an = sign, and graph the equation. If the inequality is < or >, graph the equation as a dotted line. If the inequality is ≤ or ≥, graph the equation as a solid line. This line will divide the xy- plane into multiple regions including an area which satisfies the inequality, and other do not satisfy.
