Profile
Settings
Refer your friends
Sign out
A modulus function is a function that returns a number or variable’s absolute value. It generates the number of variables’ magnitudes. Plotting such graphs is likewise a simple procedure, with the domain being all input values, such as x (all real numbers), and the range being all function values (y = f(x) = all positive real numbers and 0).
In this article, we will learn about solved examples on modulus function, its meaning, importance, and application, along with solved examples.
Meaning of Modulus Function
A modulus function determines a number’s magnitude regardless of its sign. The absolute value function is another name for it. The modulus of a real number x is given by the modulus function, represented as |x| in mathematics. It returns a non-negative value for x, implying that the function’s output is always positive, regardless of the input. A number’s modulus, or absolute value, is sometimes known as the number’s distance from the origin or zero.
The function is denoted as y = |x| or f(x) = |x|,
where f: R → R and x ∈ R.
Thus, |x| is the modulus of x in mathematics, where x is a real number. The modulus function takes the actual value of x if x is more than or equal to 0. However, if x is less than 0, the function takes the minus of the actual value ‘x’. Following this method, you can use a graph of modulus function importance.
Domain and Range of Modulus Function
The domain of a function refers to the range of values that can be put into it. This is the set of x values in a function like f(x). On the other hand, a function’s range is the set of values that the function can take. This is the set of values that the function produces when we enter an x value.
The domain of modulus function is R, where R represents the set of all positive real numbers, while its range is the set of non-negative real numbers, denoted as [0,∞) and t. Any real number can be modulated using the modulus function.
Therefore, it can be said that the range of the modulus function is [0,∞) and the domain is R.
Application of Modulus Function
You can learn about Solved Examples on Modulus. To understand the application of the formula, let us consider a few solved examples:
Solved Example: Consider the modulus function f(x) = |x|. Then:
- If x = -7, then y = f(x) = – (-7) = 7, since x is less than zero
- If x = 5, then y = f(x) = 5, since x is greater than zero
- If x = 0, then y = f(x) = 0, since x is equal to zero
Thus keeping the aforementioned rules in mind, we can solve any modulus function.
Graph of modulus function meaning
Thus, so far, we have studied the meaning, function, and application of the modulus function. The graph of the modulus function shows the relation between x and y as the values of x change. The graph is plotted in a way that: For all values of x, the range of function f(x) is positive.
For a function, y = |x|:
- The x-axis shows the value of variable x
- The y-axis shows the value of function y.
For example, let us suppose x is a variable, and f(x) = |x|
Then according to the function, the values of f(x) are shown below:
x | f(x) = |x| |
10 | 10 |
5 | 5 |
2 | 2 |
1 | 1 |
0 | 0 |
-1 | 1 |
-2 | 2 |
-5 | 5 |
Thus, when these values are plotted on a graph, the graph of the modulus function f(x) = |x| will look like this:
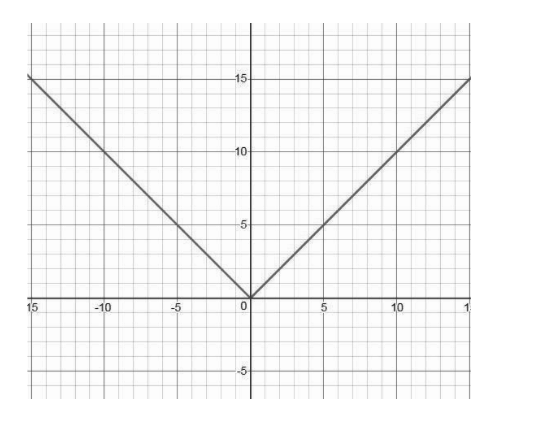
It can be seen in the graph that:
- If x = -5 then y = |-5| = 5
- If x = -2 then y = |-2| = 2
- If x = -1 then y = |-1| = 1
- If x = 0 then y = |0| = 0
- If x = 1 then y = |1| = 1
- If x = 2 then y = |2| = 2
- If x = 5 then y = |5| = 5
- If x = 10 then y = |10| = 10
Thus it can be inferred that for all possible values of x, the function f(x) remains positive.
Properties of Modulus Function
The properties of a modulus function can be iterated as follows:
Property 1: For all real values of x, the modulus function returns a positive number. It’s also incorrect to convert the modulus function to a negative number.
Thus,
|x| = a; a > 0 ⇒ x = ± a;
|x| = a; a = 0 ⇒ x = 0;
If |x| = a, then the value of a can not be less than zero.
Property 2:
Case 1: (If a > 0)
Inequality of a negative number
|f(x)| < a and a > 0 ⇒ −a < f(x) < a
Inequality for a positive number
|f(x)| > a and a > 0 ⇒ −a> f(x) or f(x) > a
Case 2: (If a < 0)
|f(x)| < a and a < 0 ⇒ there is no solution for this.
|f(x)| > a and a < 0 ⇒ this is valid for all real values of f(x).
Property 3: If a, b are real numbers, then
|-a| = |a|
|a − b| = 0 ⇔ a = b
|a + b| ≤ |a| + |b|
|a − y| ≥ ||a| − |b||
|ab| = |a| |b|
|ab| = |a||b|, where y is not equal to zero.
Conclusion
A modulus function is a function that returns a number or variable’s absolute value. It is denoted by |x|. It generates the number of variables’ magnitudes. Plotting such graphs is likewise a simple procedure, with the domain being all input values, such as x (all real numbers), and the range being all function values (y = f(x) = all positive real numbers and 0). This article told you about solved examples on Modulus.
