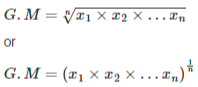Geometric Means Between Two Given Numbers

The Geometric Mean (GM) is an average value or mean that calculates the product of a bunch of numbers to indicate their central tendency. Essentially, we multiply all of the numbers and then take the nth root of the multiplied numbers, where n is the total number of data values. For example, the geometric mean of a pair of numbers such as 3 and 1 is √(3×1) = √3 = 1.732.

The summary that describes the entire data set values can be easily expressed using measurements of central tendencies in mathematics and statistics. The mean, median, mode, and range are the most essential indicators of central tendency. Among these, the data set’s mean will provide you a general overview of the data. Let us go over the definition, formula, properties, applications, and the relationship between AM, GM, and HM in this article with solved examples.

Geometric Mean: An Overview

The geometric mean is the product of n integers divided by the nth root. The geometric mean differs from the arithmetic mean, as shown below. Because we add the data values and then divide by the entire number of values in arithmetic mean. However, in geometric mean, we multiply the given data values and then take the root of the total number of data values using the radical index. Take the square root if you have two data, the cube root if you have three data, and so on. If you have four data values, take the fourth root, and so on.

Geometric Mean Formula

The following is the formula for calculating the geometric mean:

The nth root of the product of the values is the Geometric Mean (G.M) of a series with n observations.

If the observations are x₁, x₂ …. x_n , then the G.M is defined as:

Finite Geometric Progression

A finite set of terms a, ar, ar2, ar3,……arn-1  is called finite geometric progression.The sum of finite Geometric series is calculated as follows:

Sn = a[(rn – 1)/(r – 1)] if r ≠ 1 and r > 1

Infinite Geometric Progression

Terms of an infinite G.P. can be written as a, ar, ar2, ar3, ……arn-1,…….

a, ar, ar2, ar3, ……arn-1,……. is called infinite geometric series.

The sum of infinite geometric series is given by:

This is known as the sum to infinity geometric progression formula.

Conclusion

A geometric progression is a sort of progression in which each term has a fixed ratio known as the common ratio. GP is another name for it. The GP is usually written as a, ar, ar2.… , where an is the first term and r is the progression’s common ratio. The common ratio can have both negative and positive values. To find the terms of a geometric series, we only need the beginning term and the constant ratio.