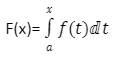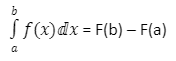The fundamental theorem in calculus is a connection between the concepts of integrating and differentiating functions. The approach is justified by computing the ratio between the antiderivative just at upper and lower limits of integration process, as stated in the fundamental theorem of calculus. Let us look at the first and second fundamental theorems of calculus, as well as evaluating the definite integral utilising the theorems, in detail in this article.
BASIC CLASSES OF INTEGRABLE FUNCTIONS:
Part 1: Integrals and Antiderivatives of the Fundamental Theorem of Calculus:
The Fundamental Theorem of Calculus defines the link between integrals and derivatives and provides a method for evaluating definite integrals without the use of Riemann sums or computing areas. The theorem is divided into two parts, the first of which is stated here: the Fundamental Theorem of Calculus, Part 1. The link between integration and differentiation is established in Part 1.
Theorem of Calculus I (Fundamental Theorem):
F'(x)=f(x) over [a, b] if f(x) is continuous across the interval [a, b] and the function F(x) is defined by
There are a few of nuanced points to be made here. First, a word or two about the notation. It’s worth noting that we’ve defined F(x) as the definite integral of another function, f(t), from point a to point x. At first glance, this is perplexing because we’ve already said that a definite integral is a number, but it appears to be a function here. The important thing to remember here is that the definite integral is a number for any given value of x. As a result, the function F(x) produces a number for each x value.
Second, Second, some of the important ramifications of this theorem are worth discussing. It’s named the Fundamental Theorem of Calculus for a reason. It not only establishes a link between integrals and derivatives, but it also ensures the existence of an antiderivative for any integrable function. It ensures that any continuous function does have an antiderivative in particular.
Part 2 of the Fundamental Theorem of Calculus:
It is possibly the most important theorem in the subject of calculus. After 500 years of hard work by mathematicians, new techniques evolved that gave scientists the tools they needed to explain a wide range of occurrences. Astronomers could now measure distances in space & map planetary orbits using calculus. Simple and accurate solutions to everyday financial challenges such as estimating marginal costs and predicting total profit are now possible. Engineers could determine a material’s bending strength or the tri motion of an object. Calculus forever altered our perspective of the world.
By comparison, using this theorem is simple after calculating approximate areas by adding the areas of n rectangles. The area like an entire curved region can be computed by simply evaluating an antiderivative at first and last endpoints of an interval, which appears almost too simple.
Part 2 of The Fundamental Theorem of Calculus:
If F(x) is any antiderivative of f(x), then
The phrase F(b)F(a) is frequently denoted by the notation F(x)|ba. This vertical bar, along with the related limits a and b, indicates that we should evaluate the function F(x) at the upper limit (in this example, b), and deduct the value of the function F(x) evaluated at the lower limit (in this case, a) (in this case, a).
If we can identify an antiderivative for the integrand, we can evaluate the definite integral by assessing the antiderivative at the interval’s ends and subtracting, according to the Fundamental Theorem of Calculus, Part 2 (commonly known as the evaluation theorem).
ANALYSIS:
When we wrote the antiderivative, we forgot to include the “+ C” word. The reason for this is that every antiderivative works according to the Fundamental Theorem of Calculus, Part 2. As a result, we picked the antiderivative with C=0 for ease of use. The constant term might have cancelled out if we had picked a different antiderivative. When assessing a definite integral, this always happens.
Figure depicts the region of area we just calculated. The region between the curve as well as the x-axis is all just below x-axis, as you can see. Even though area is always positive, a definite integral can result in a negative number. A negative number, for example, shows that the company is losing money over the provided interval if this is a profit function.
WHAT MAKES A FUNCTION INTEGRABLE?
When mathematicians talk about whether a function is integrable, they’re not talking about how difficult it is to compute the integral — or even whether a method exists. Mathematicians discover new strategies to combine classes of functions every year. This does not, however, imply that functions that were before nonintegrable are now integrable.
Similarly, whether a function’s integral may be simply written as another function without resorting to infinite series has no bearing on its integrability.
When mathematicians say a function is integrable, they simply mean that the integral is clearly defined — in other words, that the integral makes mathematical sense.
Integrability is dependent on consistency in practise: A function is integrable on a given interval if it is continuous on that interval. Furthermore, if a function on an interval has only a finite number of certain sorts of discontinuities, it is also integrable on just that interval.
Nondifferentiable functions include those with discontinuities, steep twists, and vertical slopes. Nondifferentiable functions are also discontinuous. Functions with steep curves and vertical slopes, on the other hand, are integrable.
The function y = |x|, for example, has a sharp point at x = 0, indicating that the function is nondifferentiable at about this point. The same function, on the other hand, is integrable for all x values. In the complete set, there are infinitely many examples of a function that is integrable but not differentiable.
As a result, the set of differentiable functions is a subset of the series of integrable functions, which is surprising. In reality, however, calculating the integral is more complex than computing the derivative for most functions.
Conclusion:
Integrals are indeed the values of a function discovered through the integration process. Integration is the process of obtaining f(x) from f'(x). Integrals allocate numbers to functions in such a way that describes displacement and motion difficulties, area & volume problems, and other problems that arise when little data is combined. We can find the function f by using the derivative f’ of the function f.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out