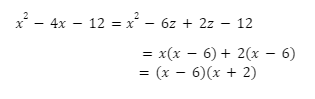FACTORISATION

Factorization can be defined as the expression which can be written as the product of factors. When we factorize an expression, we write it as a product of factors. These factors might be numbers, algebraic expressions, or algebraic variables.

Factorization can be implemented in real-life also. The examples are- calculations required while traveling, division of anything into equal parts, comparison of different prices. 

FACTORISATION-

Factorization can be defined as the expression which can be written as the product of factors. These factors might be numbers, algebraic expressions, or algebraic variables.

Let us understand the meaning of factorization through an example-

3xy,  2xy+2,  5(y+1)(x+2) are in factor form.

FACTORS-

Let us understand factors of any natural number through an example-

15=factors of 15 are 1, 15, 3,5

Thus, 1, 3, 5, and 15 are the factors of 15. Here, 3 and 5 are the prime factors.  So, A number in the form of a product of prime factors is called the prime factor. 

Sometimes, every term in a given expression does not have a common factor; but the terms can be grouped in a way so that all the terms in each group can have a common factor. When we do this, there emerges a common factor across all the groups leading to the required factorization of the expression.

A systematic way of factoring an expression is the common factor method. This method consists of three steps-

1. Writing each term of the expression as a product of irreducible factors.

2. Looking for and then separating the common factors.

3. Combining the remaining factors in each term according to the distributive law. 

FACTORS OF ALGEBRAIC EQUATIONS-

Let us take an example- 5xy+3x

The term in the above expression 5xy is formed by the factors 5, x, y can also be expressed as 

5xy=5×x×y

These factors cannot further be expressed as the products of factors. In an algebraic expression, we can use the word ‘ irreducible’ in place of prime. So, 5×x×y is the irreducible form of 5xy. 

EXAMPLES-

1. Factorize 12a2b+15ab2

Solution-  12a2b= 2 2 3a a b

15. ab2=3×5×abb  

Two terms have 3, a and b as common factors. 

 12a2b+15ab2=3 ×a×b×2×2×a+(3×a×b×5×b)

=3×a×b×[ 2×2×a +5×b]

=3ab×( 4a+5b

=3ab( 4a+5b)

FACTORIZATION THROUGH VARIOUS METHODS-

Factorization using identities-

In expression which is having factors of the type x+ax+b , the numerical term gives ab. Its factors, a and b should be chosen so that their sum, with signs taken off, is the coefficient of x. 

We know that in the case of numbers, a division is the inverse of multiplication. This is also applicable to the division of algebraic expressions. 

Let us take an example to understand this-

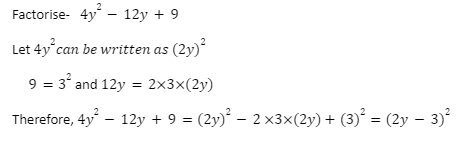
Factorization by regrouping terms –

Sometimes, every term in a given expression does not have a common factor; but the terms can be grouped in a way so that all the terms in each group can have a common factor. When we do this, there emerges a common factor across all the groups leading to the required factorization of the expression. This is called the method of regrouping.

Let us understand the factorization by the regrouping of terms through an example-

Take the expression 2xy+3+2y+3x

Before factorizing, let us understand what regrouping means. The way the expression is written, it cannot be factorized in that way. Rearranging the above expression as 2xy+2y+3x+3, will allow us to form groups like 2xy+2y and (3x+3) leading us to factorization. This whole process is called regrouping. Regrouping the above expression as 2xy+3x+2y+3. 

2xy+3x+2y+3= 2×x×y+3×x+2×y+3   

= x × 2y+3+1×(2y+3)

= (2y+3)(x+1)

In factorization by regrouping, we should remember that any regrouping i.e. rearrangement of the terms in the expression might not lead to factorization. We must observe the expression and come out with the desired regrouping by trial and error. 

Factors of the form (x+a)(x+b)-

The factors are not in the form of perfect squares. However, it seems to be of type x2+a+bx+ab.

x+ax+b=x2+a+bx+ab

Let us understand this with an example-

 Factorise- x2+5x+6

 Here ab =6 and  a+b=5The factors will be in the form of (x+ a ) and (x+ b)

If ab=6 means a and b are factors of 6. 

a=6, b=1 

a+b=7 but it should be 5. So this is wrong. 

Let a=2, b=3, then  a+b=5. This is correct. 

The factorized form will be (x+2)(x+3)

FACTORISATION METHOD OF QUADRATIC EQUATION-

A quadratic expression also can be said as quadratic polynomial is expressed in the form of ‘ax2+bx+c ‘  where a, b, c are real numbers. 

The factorization method for solving a quadratic equation is important for solving quadratic polynomials. 

Let us understand the factorization of a quadratic polynomial with an example-

FACTORISATION PROPERTIES-

There are various properties of factorization-

1. Every number is the product of 1 and the number itself. 

Like 10=2×5

 =1×10

 Here, 1, 2 , 5, and 10 are the factors of 10

2. 1 will be the factor of every number. 

Like in the previous example 1 is the factor of 10.

3. 1 will be the smallest factor of every number. 

CONCLUSION-

As discussed above we studied what factorization means, what are factors, what are the methods to do factorization, and what are the properties of factorization. Above we have discussed every aspect of factorization with examples. Talking about factors, 1 is the smallest and the only factor which will be common to every number. Every number is the product of 1 and the number itself.