The exponential and logarithmic functions are very fundamental concepts.
They are the inverse of each other and can conveniently represent a wide range of integers.
They are continuous and differentiable across their whole domain. The ease with which their derivatives are written gives you an indication of their importance in Mathematics and other sciences.
Exponential Functions
Exponential functions have the form:
f(x) = bx
Where,
b= base
x= exponent (or power);
If b is > 1, the function’s value increases as x increases.
The slope of an exponential function continually grows as x increases, which is a unique property of exponential functions.
All real numbers are included in the domain of exponential functions. All real values larger than zero are included in the range.
The line y = 0 is the horizontal asymptote for all exponential functions.
When a > 1, the exponential function grows as x grows, and as x grows less, the function shrinks. On the other hand, when 0 < a < 1: as x increases, the function decreases, and as x decreases, the function increases.
When simulating systems whose relative growth rate is constant and the natural exponential function is beneficial and relevant. Populations, bank accounts, and other similar scenarios fall within this category.
Graph of Exponential Function
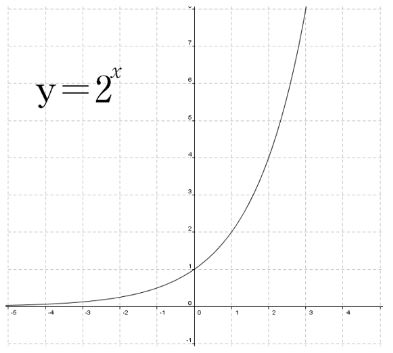
Graph of
y=2X
The graph of this function crosses the y-axis at (0, 1) and increases as x approaches infinity. The x-axis is a horizontal asymptote of the function.
Example of Exponential Function
Simplify the following exponential expression: 3x – 3x+2
Solution:
Given exponential equation: 3x – 3x+2
By using the property: ax ay = ax+y Hence, 3x+2 can be written as 3x.32
Thus the given equation is written as:
3x – 3x+2 = 3x – 3x·9
Now, factor out the term 3x : 3x – 3x+2 = 3x – 3x·9 = 3x(1 – 9)
3x – 3x+2 = 3x(-8)
3x – 3x+2 = -8(3x)
Therefore, the simplification of the given exponential equation 3x-3x+1 is -8(3x).
Logarithmic Functions
The logarithmic function is a common mathematical calculation medium.
Logarithmic functions are closely connected to exponential functions and are frequently regarded as the exponential function’s inverse. In an exponential form, the logarithm of any number X is the exponent to which the base of the logarithm should be raised in order to achieve the number X.
Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y = ax is x = ay. The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. It is called the logarithmic function with base a.
In this definition, y=logbx is called the logarithm form, and by=x is called the exponential form.
A logarithmic function has a domain of real numbers higher than zero and a range of real values. The graph of y = logax is symmetrical to the graph of y = ax with respect to the line y = x. This is true for any function and its inverse.
A logarithmic function with base e is referred to as a natural logarithmic function. f (x) = logex = ln x, where x > 0.
ln x is simply a new notation for logarithms of base e. The buttons “log” and “ln” are common on calculators. The “log” button assumes the base is ten, while the “ln” button allows the base to equal e.
The common logarithmic function is the logarithmic function with base 10. Because our numbering system is based on ten, it is commonly used. In calculus, natural logarithms appear more frequently.
Properties of logarithms:

Graph of logarithmic function
Relation between exponential and logarithmic functions
Logarithmic and Exponential are inverse functions to each other. Logarithmic function undoes what is done by the exponential function.
Ex: exponential function 2^3 = 8
So, the Logarithmic function will tell the value by which when 2 is powered, it gives output as 8.
So, it is shown as log2(8) = 3
So, both Logarithmic and Exponential show inverse function to each other.
Examples:
- Solve this equation for x : 5x+1 = 625.
Solution:
When the unknown x appears as an exponent, then to “free” it, take the inverse function of both sides.
In this example, take the logarithm with base 5 of both sides.
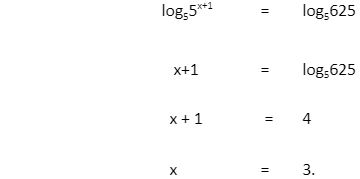
In general, if we have any equation,
f(x) = a,
then if g is the inverse of f:
x = g(a)
Conclusion
Exponential and logarithmic functions are interrelated and have many real-world applications. For e.g., logarithmic functions are helpful when it comes to measuring the magnitude of earth, the loudness of sound, acidity, alkalinity of products, and much more. In the same way, the exponential functions help measure/calculate bacterial growth/decay, population growth/decline, and compound interest.
Certain properties of logarithmic and exponential functions, as mentioned above, help us to understand the correlation between them and help us to solve their problems.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






