Profile
Settings
Refer your friends
Sign out
The famous mathematician Leonhard Euler thought solving equations such as x² + n² = 0, n belongs to Z was impossible. Later the mathematician Leonhard Euler came up with creating a number that could solve such equations.
In 1777, Euler made the symbol i stand for 1, making it easier to understand. Then in 1806, Jean Robert Argand wrote how to plot them in a plane, and today the plane is called the Argand diagram. Today, it is very useful in the world. Every engineer uses it to study beams’ stresses and to study resonance. Complex numbers come to use many things such as studying the flow of fluid around objects and a pipe. Complex numbers are also frequently used in electric circuits and help transmit radio waves. We can conclude that if it were not for it, we might not be able to talk via mobile or listen to the radio.
The History Behind The Creation
In 1545, Girolamo Cardano wrote a book entitled Ars Magna, which means Great Work. On solving the equation x(10-x) = 40, he found the
answer 5 plus or minus -15. Although he found the answer, he intensely disliked imaginary numbers.
Later, in 1637 a mathematician named Rene Descartes tried to develop a standard form of complex numbers as a + ib. Rene Descrates’ theory was agreed by Issac Newton, but on the other hand, Albert Girad went to call these “Solutions impossible. Among all the believers, there also was Rafael Bombelli. He also helped introduce them, but since he could not find out how to put them to use, he mostly did not believe them. Later in 1777, Euler made the symbol i stand for 1, making it easier to understand. Then in 1806, Jean Robert Argand wrote how to plot them in a plane, and today the plane is called the Argand diagram.
Radius of Curvature
We are familiar with complex numbers of the form z=a+ib. Some alternate forms are also helpful. When representing complex numbers geometrically, we assume the x-axis to be the real part of the complex number and the y-axis to be the imaginary part of the complex number. The XY plane is considered the complex plane.
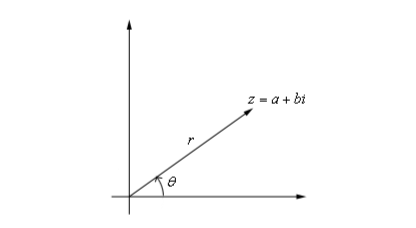
In the above figure, z is assumed as a non-zero complex number z=a+ib. (a,b ) are the points on the XY plane they can also be represented as polar coordinates (r,) where r is the distance of the point (a,b) from the origin and is the angle from the positive x-axis to the line connecting the origin to the point (a,b).
If we pick any possible argument value for a given complex number z, let us assume θ. If we increase the value of θ, which is generally just increasing the angle that the point (a,b) makes with the positive x-axis, we rotate the point about the origin in an anticlockwise manner. We know that it takes 2π radians to make one complete circle. That means we will be back at your initial position when we reach θ+2π.
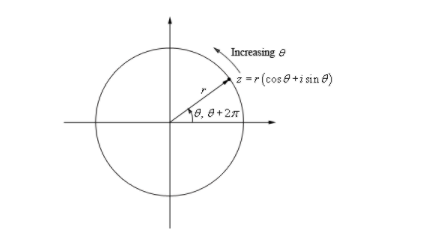
Euler’s Form Of A Complex Number Meaning
The Euler formula was created by the mathematician Leonhard Euler. In complex numbers, Euler’s formula is used to rewrite the polar form of a complex number as its exponential form.
The original Euler formula is as follows:
=> eiθ=cosθ+isinθ
Using this Euler formula, we can write represent any complex number in the form:
=> z=reiθ
Here is arg z; infinite exponential forms exist for a given complex number.
We can also write the exponential form as:
z=rei(θ+2πn)
where n= 0,1,2,3,4,5,6……
where θ can be any value of the argument.
To obtain the value of r, we can use z= |z|(cos+isin) to write the exponential form.
Another way around is to take the direct approach. That is be taking the modulus of both sides and then simplifying it further as follows,
|z| = ∣reiθ∣ = |r| |eiθ| = |r| |cosθ + isinθ| =r2+0 cos2θ+ isin2 = r
here, we can see that r=|z|.
Conclusion
Euler’s identity is believed to be an example of the beauty of mathematical relations as it shows us a connection between the most fundamental numbers in mathematics. It is also directly used to prove that π is transcendental; it implies that it is impossible to square a circle. Today, it is very useful in the world. Every engineer uses it to study beams’ stresses and to study resonance. Complex numbers come to use in a lot of things such as studying the flow of fluid around objects and a pipe. Complex numbers are also frequently used in electric circuits and help transmit radio waves. We can conclude that if it were not for it, we might not be able to talk via mobile or listen to the radio. Also, every polynomial equation has a solution if complex numbers are used. It is good that it was created.
