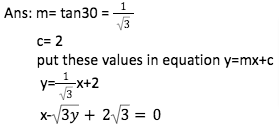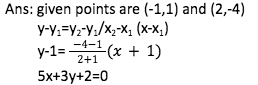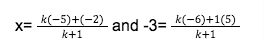INTRODUCTION
A straight line has only one dimension without any breath. When there is no turning point in between two points then it’s called a straight line. In other words we can say that the shortest distance between two points is known as a straight line.
In this topic we learn the concepts of lines like slopes , angle b/w two lines , equation of line.
Now let us look forward and start learning in detail about straight lines and their equation , equation of plane , point form , intercept form and also solve some questions that are frequently asked and see the graphs of point slope , intercept and much more . Now we will start studying in depth.
DEFINITION AND EQUATION OF PLANE
Plane is two dimensional surface that extends indefinitely. The general form of plane is ax+by+cz+d=0 here, a, b and c are the components of normal vector n=(a , b , c)
DEFINITION AND EQUATION OF LINE
When there is no turning point in b/w the two points are said to be straight lines. Or we can say that a straight line has only one dimension as we talk about it early.
EQUATION OF LINE
The general equation is
ax+by+c=0
here x&y are variables and a,b,c are constants.
INTERCEPT FORM OF LINE
The equation of line which cuts off intercepts a and b from x-axis and y-axis.
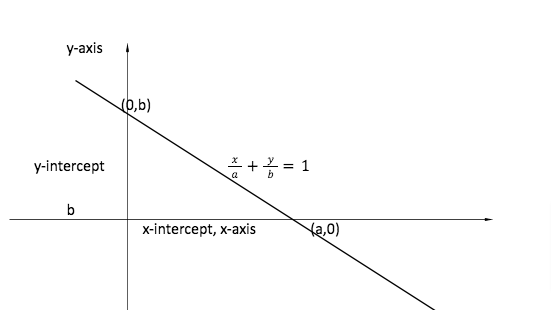
POINT FORM
Let the equation of x-intercept is ‘a’ and y-intercept is ‘b’
TWO POINT FORM
The equation line when passes through the points (x1,y1) and (x2,y2) is
y-y1 = y2-y1 (x-x1)
x2-x1
OR
y-y2 = y2-y1 (x-x1)
x2-x1
(x1,y1) and (x2,y2) two points on a line (x,y) are variables.
SLOPE OF LINE
The slope of straight line is tanƟ
y=mx+c
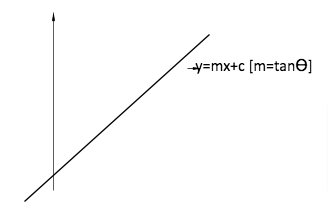

When the line is parallel to the x-axis then the slope is 0.
When the line is parallel to the y-axis then the slope is undefined.
SLOPE OF LINE WHEN PASSING FROM TWO GIVEN POINTS
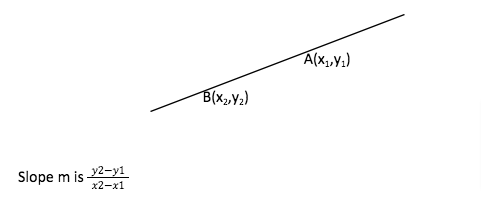
RELATION BETWEEN TWO LINES
Assume P1 and P2 are two lines
P1 = a1x+b1y+c1=0
P2 = a2x+b2y+c2=0
- a1/a2 =b1/b2 ≠ c1/c2
when two lines are parallel lines
- a1/a2 ≠ b1/b2
when two lines intersect a point
- a1/a2 =b1/b2 =c1/c2
when the lines are coincident
ANGLE BETWEEN TWO LINES

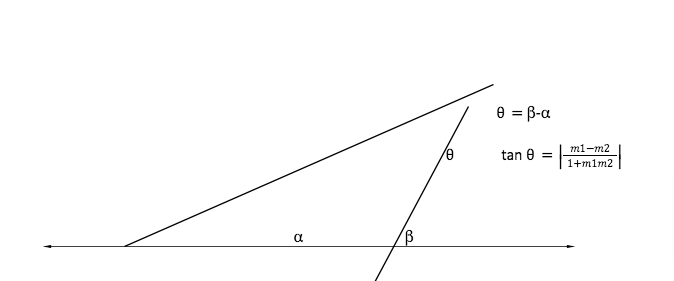
THE ANGULAR BISECTOR OF STRAIGHT LINE
Let the P1 = a1x+b1y+c1 = 0
And P2 = a2x+b2y+c2 = 0
When the angle of bisector containing the origin then the equation is:
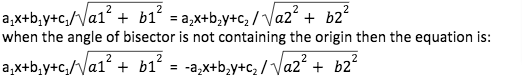
THREE LINES CONCURRENCY
Let assume the lines be
P1 = a1x+b1y+c1 = 0
P2 = a2x+b2y+c2 = 0
P3 = a3x+b3y+c3 = 0
And concurrency of lines condition is
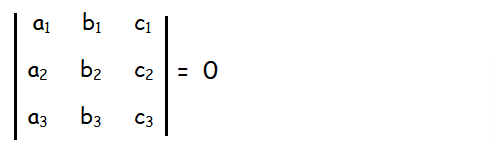

CONCLUSION

 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out