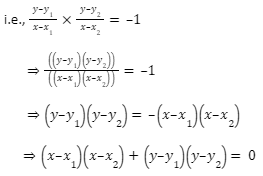Profile
Settings
Refer your friends
Sign out
A circle is a shape made up of all points in a plane that are at the same distance from a central point. It’s the curve drawn out by a point moving in a plane while keeping its distance from a particular point constant. The radius is the distance between any point on the circle and the centre. A positive integer is usually necessary for the radius. A degenerate case is a circle with display style r=0. Except when otherwise specified, this article is about circles in Euclidean geometry, specifically the Euclidean plane.
Definition of Circle
A circle, in particular, is a closed curve that splits the plane into two regions: interior and exterior. In ordinary usage, the phrase “circle” can refer to either the figure’s boundary or the entire figure, including its inside; in strict technical terms, the circle is merely the boundary, and the entire figure is referred to as a disc.
A circle is also a special type of ellipse in which the two foci are coincident, the eccentricity is 0, and the semi-major and semi-minor axes are equal; or the two-dimensional shape enclosing the maximum area per unit perimeter squared, using the calculus of variations.
Diameter of a Circle
A diameter is a line that travels through the centre of a circle and intersects the circumference at opposing ends. It measures twice as long as the circle’s radius. In other words, a circle’s diameter is the line that goes through its centre and divides it into two equal halves.
The diameter of a circle is equal to twice the radius’s length. The radius of a circle is measured from its centre to one of its endpoints on the circle’s perimeter, whereas the diameter is measured from one end of the circle to the other end of the circle, passing through the centre. The letter D stands for it. The circumference of a circle has an unlimited number of points, which means the circle has an infinite number of diameters, each of which is of equal length.
Equation of a Circle in Which Endpoints Are Given
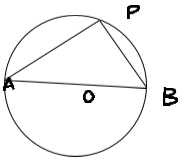
As indicated in the diagram, A(x1,y1) and B(x2,y2) are the endpoints of the circle’s diameter.
Let6, any point on the circle be P(x,y). So,the angle formed by connecting the points A and B with the point P is 90 degrees. To begin, we calculate the slopes of the lines PA and PB as follows:
As the lines PA and PB are perpendicular to each other (since m∠APB=90°. As a result, the product of their slopes equals –1.
So, this is the required equation of the circle when end points of the diameter are given.
Conclusion
Circles have a vital role in both Geometry and Mathematics in general. Several theorems relating to circles are frequently used in exams and even in real-life circumstances such as building and architecture. Experts always rely on the terms and concepts covered in this detailed text to put them into practise. Circles will very certainly make up a large portion of your Maths curriculum, and missing this topic will cost you valuable marks that may otherwise be readily earned. To achieve good grades in your tests, it is recommended that you read over and internalise as many formulas and properties relating to circles as possible.
