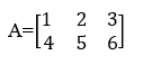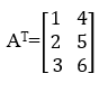In mathematics, an elementary matrix is a matrix that differs from an identity matrix by a single elementary row operation. If F is a field, the elementary matrix produces the general linear group GLn (F). The left multiplication (pre-multiplication) using the elementary matrix represents the operation of the basic row, and the right multiplication (post-multiplication) represents the operation of the basic column.
The basic row operation is used in Gauss-Jordan to reduce a matrix to a row echelon form. These are also used in the Gauss-Jordan method to further reduce the matrix into row echelon forms.
Matrix:
A matrix, a set of numbers arranged in rows and columns to form an array of rectangles. Numbers are called matrix elements or entries. Matrices have a wide range of uses in various fields of engineering, physics, economics, statistics, and mathematics. Matrix also has important uses in computer graphics that have been used to represent image rotation and other transformations.
Historically, the first thing recognized was not the determinant, but the specific number associated with the arrangement of the squares of numbers called the determinant. The idea of the Matrix as a unit of algebra gradually emerged. The term matrix was introduced by the British mathematician James Sylvester in the 19th century, but it was his friend Arthur Cayley who developed the algebraic aspect of the matrix in two papers in the 1850s. Cayley first applied them to the study of systems of linear equations, but they are still very useful. As Cary recognized, a particular set of matrices forms an algebraic system in which many of the usual arithmetic laws (such as associative and distributive laws) hold, but other laws (such as commutative laws) are invalid. So, these are also important.
Elementary matrix:
An elementary matrix is a matrix obtained from an identity matrix by applying an elementary row operation to the identity matrix. A series of basic row operations transforms a matrix into a row echelon form. The first goal is to show that you can perform basic row operations using matrix multiplication. The matrix E = [ei,j] used in each case is mostly an identity matrix. The product EA performs the corresponding basic row operation on A.
Transpose of a Matrix:
The new matrix obtained by exchanging the rows and columns of the original matrix is called matrix transpose. If A = [aij] is an m × n matrix, the matrix obtained by swapping the rows and columns of A will be the transposed matrix of A. This is represented by A’ or (AT). That is, if A = [aij] m x n, then A’= [aji] n x m.
For Example,
Next is the transpose of A
The transpose of matrix A can be thought of as a matrix formed by rearranging rows into columns and columns into rows. These swaps the indexes of each element. An important property of matrix transpose makes it easy to manipulate the matrix. Also, some important transposed matrices are defined based on their characteristics. If the matrix is equal to its transpose, then the matrix is considered symmetric. If the matrix is equal to the negative number of transposes, the matrix is considered skew symmetric. A matrix conjugate transpose is a matrix transpose in which the elements have been replaced with complex conjugates.
Order of Transpose Matrix:
Matrix order represents the number of rows and columns in a particular matrix. All horizontal lines of an element are called rows of a matrix and are indicated by n, and vertical lines of an element are called columns of a matrix and are indicated by m. Together they represent the degree of the matrix written as n × m. And the transposed order of the given matrix is described as m*n.
Elementary Operations:
A matrix is a rectangular array of numbers. That is, the numbers grouped into rows and columns. Matrix is used to represent and solve simultaneous linear equations. There are three types of elementary matrix operations.
- Swap two rows (or columns).
- Multiply each item in the row (or column) by a non-zero number.
- Multiply the row (or column) by a non-zero number and add the result to another row (or column).
- When these operations are performed on rows, they are called basic row operations. Also, when performed on columns, they are called basic column operations.
Elementary Operators:
All types of basic operations can be performed by matrix multiplication using a square matrix called the basic operator.
How to Perform Elementary Row Operations:
Perform the basic row operations on the A, rxc matrix by performing the following steps:
To find the basic row operator E, apply this operation to the rxr identity matrix.
To perform a basic row operation, premultiply A by E.
Conclusion:
Fundamental line operations are used to transform a system of linear equations into a new system with the same solution as the original system (that is, to an equivalent system).
There are three basic operations.
- Multiplies the equation by a non-zero constant.
- Adds a multiple of one equation to another.
- Swap the two equations.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out