Domain Codomain

Domain in mathematics is very common and used in the subject of relation and function. The domain is basically the set of all the values for which a relation or function is defined. Let us say the relation is defined as below:

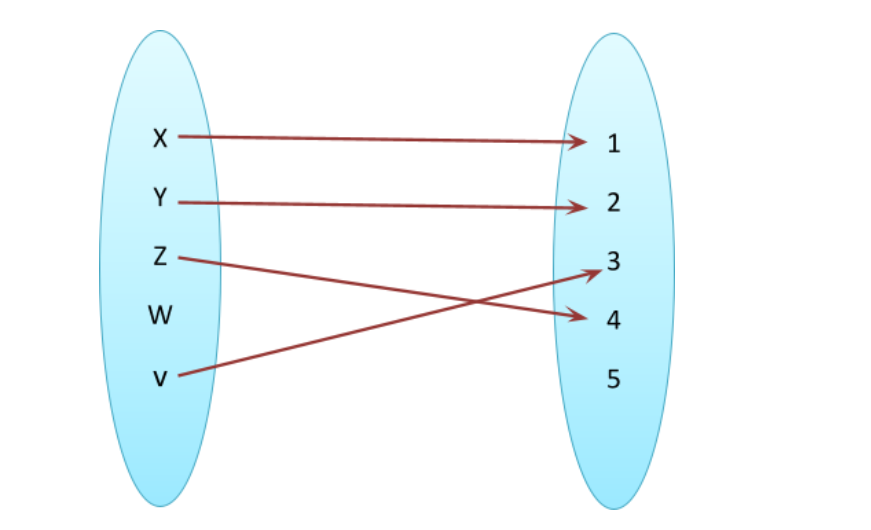
In the above example, it is defined only for x, y, z, and v and hence it is the domain of function. The function is not defined for value w. So, w is not included in the domain of above relation. 

The domain set can be written as {x, y, z, v}. The corresponding range will be {1, 2, 3, 4}. Here, 5 is not in the range as it is not mapped with any domain value. 

In the above example, each member of the domain set is mapped with a unique value of the set in range. So the above relation is also a function. Whenever two or more than two values of a domain are associated with the same value of range then it is not called function. However, domain is defined for both relation as well as function. The following example showed the domain and range for a relation which is not a function.

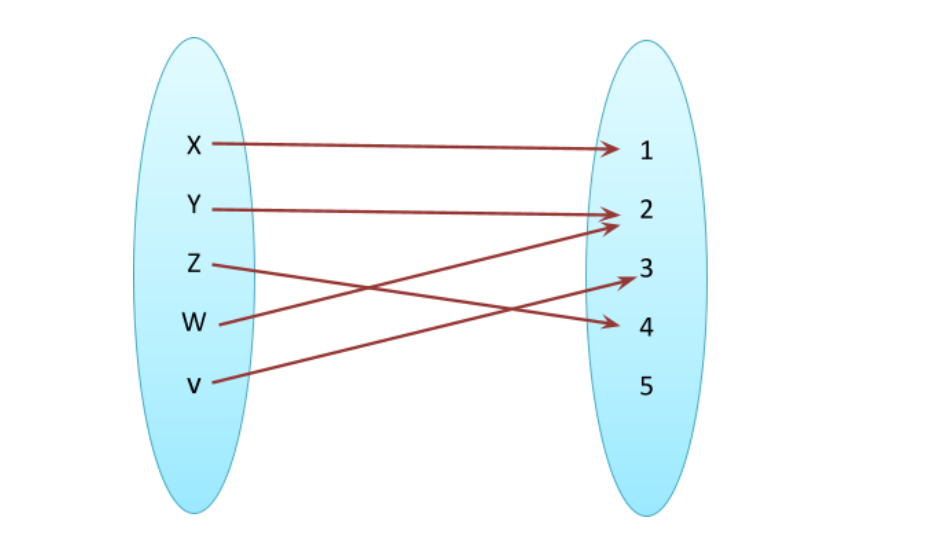
In the above example, the domain is {x,y,z,w,v} as the above relation is defined for all values of the set. However, y and w are mapped with the same value of range 2. So, the above is not a function. It is just a relationship. In very simple words, we can say that the domain is all those values which go into a function, and the range is all those values which come out. But in fact they are very important in defining a function.

We can also say that a function relates an input to an output. Example: Suppose a tree grows 40 cm every year, therefore, the height of the tree is related to its age. Using the function h:

h(age) = age × 40

So, if the age is 20 years, the height is h(20) = 800 cm

If we are saying that, “h(20) = 800” it means we are saying that 20 is related to 800.

Input and Output

But in some cases all values may work!

• The function may not work, if we will give it the wrong values (such as a negative age) etc.
• And knowing the values that can come out (such as it should be always positive) can also help.

So we need to say all the values that can go into and come out of a function.

This can be done in a better way using sets. 

In fact, a function is defined in terms of sets also. 

In more complex functions, domain is defined as the set of all the values for which a function is defined. 

Codomain:

In a function, domain and range are clearly defined. However, codomain has little difference with range of function. Let us try to understand codomain in a better way. Codomain is basically the set of all possible values which might come with a given set of domain. Range is the set of value which actually comes with given domain and defined function. In this way, the range is a subset of the codomain.  The another way to differentiate range and codomain is when we might know that what might be the range of a given function that is codomain however exact output is not known such as if real numbers are codomain of a given function is well known however exact values are only known when domain values are actually put in to the function.

Going into the complex examples, let us take the example of f(x) = x2+1. So, we can say that the function is defined for all real values of x. so, all real values are the domain of function. Also, we can say that the range of functions will also be real values which can be said to be codomain. However, we can see that f(x) can have only positive values for any values of x. So, the range of functions includes only positive real numbers.

Let us take another example, f(x) = 1x-2.

Here, f(x) is defined for all values of x except x=2. So, the domain of the function includes all real values of x other than x=2.  

Conclusion:

Based on above discussion, Domain and Codomain can be put as follows:

1. Domain: All the values for which a relation or function is defined.
2. Codomain: The values which may come out when domain values are put as per given relation or function.