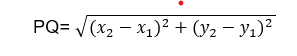Profile
Settings
Refer your friends
Sign out
Distance is a mathematical term that describes how far two points in a two-dimensional space are apart. One of the essential mathematical quantities is this parameter. It’s used to simulate things like a moving body’s velocity, the amount and direction of electrical and gravitational forces, and signal processing in advanced mathematics and physics. Let’s take a closer look at the distance between the two spots.
Distance Formula in Maths
A line segment connecting the two points is used to calculate the separation between them. It can be calculated how far two points are from one another in coordinate geometry by figuring out how long a line segment is that links the two coordinates.
We will now examine the formula for finding the distance between two locations in a two-dimensional or three-dimensional plane.
What is the length of a line connecting two points?
In all circumstances, the distance between two places is given by the length of the line segment connecting them. A single line serves as the only link between the two locations in this situation. By computing the length of a line segment, one can determine the distance between two locations.
The distance between two places is quantified by the length of the line segment that connects them (but this cannot be the length of the curve joining them). In other words, regardless of their proximity, the distance between two different places is always greater than 0.
The Formula for the Distance Between Two Points
It is possible to compute the distance between two places using the supplied coordinates by applying the distance formula to the data. We may either use the 2D distance formula or the Euclidean distance formula to calculate the distance between any two points in the 2-D plane.
The distance between two locations and the middle of the distance between two points:
In mathematics, the distance formula is an algebraic statement that is used to calculate the distance between two locations having the coordinates P(x1, y1) and Q(x2, y2).
PQ= (x2-x1)2+(y2-y1)2
Distance Formula Derivation
For the purpose of deriving the formula for calculating the distance between two points on a two-dimensional plane, let us suppose that there are two points with the coordinates as follows:
A(x₁,y₁) B(x₂,y₂)
Following that, we will suppose that the line segment between A and B is a straight line. Form a triangle by making the third point at C.
The Pythagorean theorem may be used to the ABC: AB² = AC² + BC²
Thus, the distance formula for determining the distance between two places is accurate. We can develop the formula for finding the distance between two points in the 3D plane using the same techniques and concepts.
Example
- Calculate the distance between P(-1, 1) and Q(1, 1).
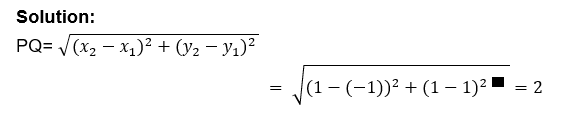
The distance between P and Q is 2 units.
This may be handled by simply inserting our x- and y-values into the distance calculation as follows: It is sometimes necessary to locate the point that is precisely between two other locations in order to solve a problem. The “midpoint” is the point in the centre of the circle. A midpoint of a line segment is defined as the point on a line segment that splits the segment into two congruent segments.
- In mathematics, the distance formula is an algebraic statement that is used to calculate the distance between two locations having the coordinates (x1, y1) and (x2, y2) (x2, y2).
Conclusion
We have studied that distance between two points is measured in feet and metres. In coordinate geometry, determining the length of a line segment that links two points may be useful in determining the distance between the locations. Learning how to compute distances between two points in two and three dimensions is now necessary.
