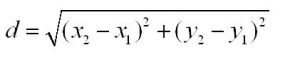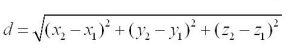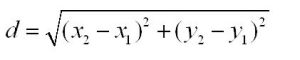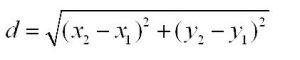Distance between points

The length of the line segment connecting the specified coordinates can be used to compute the distance between two points in coordinate geometry.The study of geometric figures using coordinate axes is known as coordinate geometry. Straight lines, curves, circles, ellipses, hyperbolas, and polygons can all be readily drawn and scaled in the coordinate axes. Furthermore, using the coordinate system to work algebraically and examine the attributes of geometric figures is referred to as coordinate geometry. Let’s look at the formula for calculating the distance between two points in a two-dimensional and three-dimensional plane. In the coordinate system, we use two very important terms and these are abscissa and ordinate. The abscissa in coordinate geometry means the horizontal (x) axis of a normal two-dimensional graph, whereas the ordinate refers to the vertical (y) axis.

The abscissa or x coordinate of a point is its distance from the y-axis when scaled with the x-axis. The ordinate is the distance between a point and the x-axis, scaled with the y-axis.

If (x, y) is an ordered pair, then y is the ordinate in this case. An ordered pair is used to represent a point in the Cartesian plane, and the abscissa is the initial coordinate (x) in the plane. The abscissa or x coordinate of a point is its distance from the y-axis scaled with the x-axis.

Let us first understand what is Distance,

Definition of Distance

Distance is a numerical value of the distance between two objects or points. The overall movement of an object, without mentioning the direction, is termerd to as distance. We defined distance as the value of ground covered by an item, regardless of its starting or ending position. And now let us understand the meaning of point in mathematics,

Definition of Points

A point is a primordial concept in traditional Euclidean geometry that describes an exact point in space and has no length, width, or thickness.

The distance between Two Points

The length of the line segment joining the two points is the distance between them. There’s just one line that connects the two points. So, evaluating the length of the line segment joining two points can be used to compute the distance between them.

The length of the line segment joining two points is the distance between them (but this CANNOT be the length of the curve joining them). It is important to note that the distance between two points is usually positive. After understanding the concept of distance, points, and distance between two points lets us understand how to calculate the distance between two points by using distance formula.

Distance Formula 

With the knowledge of distance, lets us calculate the distance between two point using distance formula,

Let say we have two point A (X₁, Y₂) and B( X₁, Y₂ )

Then the formula of distance formula in 2D is :

Also the Distance formula in 3D is :

Conclusion

• The length of the straight line joining two points in the coordinate plane is used to calculate the distance between them. Because this distance can never be negative, we use the absolute value when calculating the distance between two points.

• The length of the straight line connecting two points can be used to compute the shortest distance between them. We can use the distance formula to calculate this distance based on coordinates in a two-dimensional or three-dimensional plane.

• The Pythagorean theorem can be used to compute the distance between two points in the cartesian plane. The hypotenuse (the line connecting the two points) can be used to make a right-angled triangle. The perpendicular and base will be lines parallel to the x and y axes, with one end as one of the specified positions and the other end as the point where they intersect. We may find the length of the hypotenuse by applying Pythagoras’ theorem, (hypotenuse)2 = (base)2 + (perpendicular)2, to the given coordinates of two points. The distance between two points is equivalent to this length.