Direct and inverse variation problems have an extensive application in different fields apart from mathematics, like physics. Many concepts of physics apply concepts of direct and inverse variation.
In this article, we will explain the problems based on the relationship between speed, distance and time, which is one of the fundamental concepts of physics. Speed, distance and time directly apply to direct and inverse variations. In the speed, distance and time relation, changing the value of one of the quantities alters the value of another. Hence, solving speed, distance and time relationship problems is one of the best ways to understand the concept of direct and inverse variation.
Definitions of direct variation and inverse variation
- Direct variation: Direct variation is a mathematical relation between two variables that are expressed by an equation in which one variable is equal to the constant times the other variable.
- Inverse variation: Inverse variation is a mathematical relation between two variables where the product of two variables is equal to a constant.
Relationship between speed, distance and time
Speed, distance and time are concepts where direct and inverse variation is extensively used. Understanding proportionality makes solving the questions containing speed, distance and time easy.
The relation between speed, distance and time is as follows:

If we observe carefully, it is clear that speed, distance and time are proportionally related to each other.
- Speed is inversely proportional to time. That means as the speed increases, the time required to travel a certain distance decreases.
- Speed is directly proportional to distance. Therefore, as the speed increases, the distance travelled also increases.
Problems based on the relationship between speed, distance and time
When you encounter direct and inverse variation problems questions involving speed, distance, and time, the question will require you to find out the value of one of three physical quantities. To get the value of either speed, distance or time, some basic information about the other two will be provided.
For example, the question might tell you that the object travels at a constant speed. Most problems will give you information about the two variables, and then it will ask you to find the value of the third variable.
When solving questions based on speed, distance, and time, always focus on the units required in the final answer. So, knowing the conversion of units is essential.
Problem: Bernie boards a train at 1:00 PM and gets off the train at 5:00 PM. During this trip, the train travelled a distance of 360 kilometres. What was the train’s average speed in kilometres per hour?
In the above question, we have the information related to the time the train travelled, which is T= 5 – 1 = 4 hours. Apart from the time, we also know the distance travelled by the train, which is 360 km. Now, using the relationship between speed, distance and time:

Problems based on inverse proportionality
Inverse variation is a mathematical relation where the increase in the value of one variable decreases the value of the other variable.
Problem: A contractor assigns 48 workers to build a wall. The workers can finish the task in 12 days. But due to some issues, only 16 workers turn up. How many days will 16 workers take to finish the same task?
Answer: In this particular problem, there are two quantities. The first quantity is the number of workers and the second quantity is the number of days.
Number of workers (x) = 36
The number of workers that turn up for the task (a) = 16
Number of days taken by 36 workers to complete the task = 12
Let the number of days taken by 16 workers to complete work be equal to y.
Now, as the number of workers decreases, the days required to complete the task will increase.
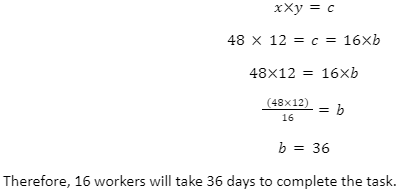
Problems on direct variation
Problem: In a direct variation formula, the constant of variation k has the quantity 6k = 60. If a variable ‘y’ have a value of 90. What is the value of x?
The general form of direct variation is y = k x. Therefore, using this equation:

Now that we have found the value of k, we will insert this value in the first equation. Moreover, we will also put the value of y in the first equation and determine the value of x.

The value of x is 9 in the above question. Thus, if you know y=k ×x, then solving direct and inverse variation problems becomes very easy.
Conclusion
Direct and inverse variation is a concept that is applicable in real-life problems. To solve direct and inverse variation problems, you must know some key concepts, such as—two variables are directly proportional to each other if they have a constant ratio, and two variables are inversely proportional when they have a constant multiple. In many instances, a variable also varies directly or inversely with multiple variables, and this relationship is called joint variation.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






