Profile
Settings
Refer your friends
Sign out
Calculus isn’t complete without derivatives. They assist us in determining the rate of change, maxima, and minima of functions. The first form of the derivative is defined as a derivative that is given by employing limitations. We already know how to calculate the derivatives for conventional functions, but there are occasions when we need to deal with complex mathematical functions that are made up of many functions. Calculating the derivative of such functions becomes difficult and time-consuming. Learning the rules and strategies that make our calculations easier becomes vital. One of them is the chain rule, which allows us to compute complex function derivatives. Let’s take a formal look at this rule.
Differentiation
Differentiation is a derivative of the value of an independent variable that can be used to determine features in an independent variable per unit alteration.
Assume f(c) is a real function and c is a domain point. At c, the derivative of f is defined as
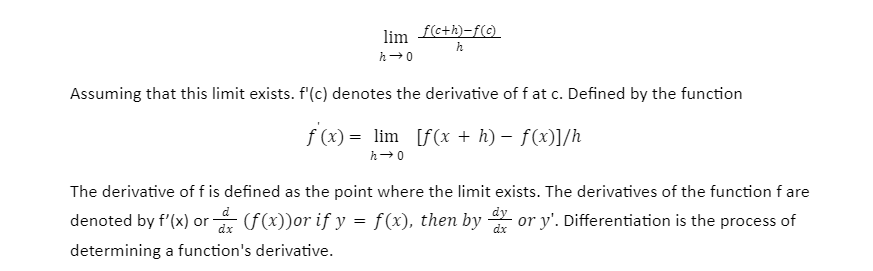
Derivatives of composite function
The product of the derivative of f(x) with respect to g(x) and the derivative of g(x) with respect to the variable x can be used to find the derivative of a composite function h(x) = f(g(x)). The derivatives of composite functions are calculated using the following formula:
If f and g are differentiable, derivative of f and g
(f o g )’ = d/dx[f(g(x))g’(x)=(f’ o g ).g’
Rules for Compound Functions
1.sum or difference rule
If the function whose derivative must be calculated is the sum or difference of two functions, the function’s derivative is the sum or difference of the two functions’ individual derivatives.
F(x) = f(x) ± g(x)
F’(x) =f’(x) ± g’(x)
2.product rule
The derivative of a function is provided by: If the function in question is the product of two independent functions, the derivative is given by:
F(x) = f(x) * g(x)
F’(x) = f’(x) * g(x) + f(x) * g’(x)
3.Quotient Rule
The derivative is calculated as follows if the function whose derivative is to be determined is the division of two functions:
F(x) = f(x)/g(x)
F’(x) = f’(x)*g(x) – f(x)*g’ (x)/g(x)2
4.Chain rule
A replacement method is sometimes used to solve complex functions. If y = f(x) = g(z) and z = h(x), the following is true:
dy/dx = dy/dzdz/dx
Differentiation’s Applications in Real-Life Problems
Differentiation is useful in the actual world. Differentiation is defined as a change in one quantity in relation to a change in another. The following are some examples of real-world applications:
The change in velocity as a function of time is known as acceleration.
A derivative function is used to find the tangent and normal to a curve.
Maximum and minimum points on a graph to be utilised in business and other studies. It’s also used to figure out how much the temperature has changed.
Conclusion
Differentiation is a derivative of the value of an independent variable that can be used to determine features in an independent variable per unit alteration.f‘x= [fx+h-f(h)]/h . The derivative is the first of calculus’ two basic tools (the second being the integral). The instantaneous rate of change of a function at a point in its domain is called the derivative. The slope of the tangent line to the graph of the function at that moment is the same as this. The concept of limit is required to establish a solid definition for the derivative.
