Profile
Settings
Refer your friends
Sign out
INTRODUCTION
The method of finding the derivatives of any specific trigonometric function is known as the differentiation of trigonometric functions. In other words, the differentiation of trigonometric functions is finding the rate of change of the function with the variable. Differentiation of trigonometric functions is a mathematical procedure for deciding the rate of change of the trigonometric functions concerning the angle variable. The method of finding the derivatives of circular trigonometric functions is often comprehended as the differentiation of trigonometric functions. The six basic functions of trigonometry includes: sine (sin x), tangent (tan x),cosine (cos x),cotangent (cot x), cosecant (cosec x) and secant (sec x).
What is the Differentiation of Trigonometric Functions?
Differentiation of trigonometric functions is a special mathematical procedure of deciding the rate of change of the trigonometric functions with respect to the varying angle. The differentiation of trigonometric functions can be done using the derivatives of sin x and cos x by using the rule of the quotient. The differentiation formulae of the basic six trigonometric functions are given below:
Proof of Derivatives of Trigonometric Functions- We will derive and prove the derivatives of trigonometric functions using various procedures such as the first principle of differentiation, chain rule, and rule of quotient along with some formulae of limit.
Derivative of sin x
The derivation of sin x by utilizing the first principle method of differentiation, that is, using the limit’s definition. To derive the differentiation of the trigonometric function sin x, we will use the limit and formulae of trigonometry:
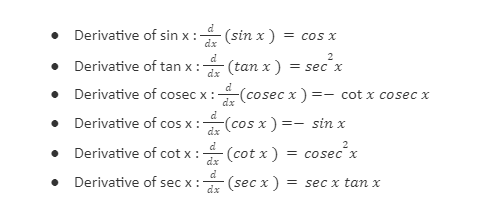
The derivation of cos x by utilizing the first principle method of differentiation, that is, using the limit’s definition. To derive the differentiation of the trigonometric function cos x, we will use the limit and formulae of trigonometry:
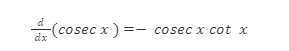
Applications of Differentiation of Trigonometric Functions
The differentiation of trigonometric functions has diverse applications in the field of engineering, physics, mathematics, and real life:
- It enables us to establish the equation of the tangent line or normal line of a curve
- Differentiation of trigonometric functions have various applications in diverse fields such as computer programming, electronics, and modeling different cyclic functions
- The derivatives of trigonometric functions are often used to establish the maximum and minimum values of certain specific functions
- It is utilized to define the slope of the tangential line to a trigonometric curve y = f(x)
- It is utilized to define the slope of the normal line to a trigonometric curve y = f(x).
Differentiation of Inverse Trigonometric Functions
The differentiation of inverse trigonometric functions is done by designating the function equal to y and applying implicit differentiation procedure on it. Below is the list of derivatives of the inverse trigonometric functions with their respective domains:
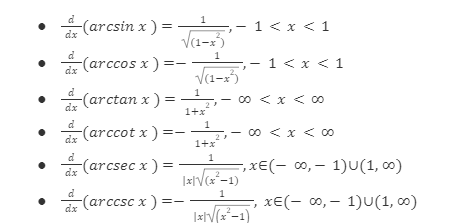
Conclusion
In this article, we have gained information regarding the derivatives of trigonometric functions, differentiation of trigonometric functions, and their validations which is done by using different rules and associated identities. We also learned to derive trigonometric functions using various properties and rules of various functions. The differentiation of trigonometric functions can be done using various associated procedures of differentiation, including the first principle of derivatives, rule of the quotient, product rule, and chain rule. Finally, we also found how to use them with the help of various examples. The differentiation of trigonometric functions has diverse applications in the field of physics, engineering, mathematics, and real life.
