Profile
Settings
Refer your friends
Sign out
Differentiation is one of the most essential subjects in maths, both intellectually and in terms of mark weightage. The term “differentiation” refers to the process of determining a function’s derivative. It is the method of finding the rate of change of a function based on the variables in the function. We can find rates of change using differentiation. It enables us to determine the rate of change of velocity with respect to time, for example (which is acceleration). It also allows us to calculate the rate of change of x with respect to y, which is the gradient of the curve on a graph of y against x. Many engineering and science problems require derivatives, particularly when modelling the behaviour of moving objects.
What is differentiation?
When a function’s derivative is expressed in terms of an independent variable, the word “differentiation” is used in mathematics. The term “speed” is synonymous with the term “slope,” which is nothing more than the instantaneous rate of change of distance over a given amount of time.
Let f(x) represent a function of x, and y represent another variable.
dy/dx the change in y per unit change in x reflects the rate of change in y
The function f(x) is defined as, if it undergoes an infinitesimal change of h near any point x.
Lim f(x + h) – f(x)/ h
The value of h tends to be zero.
differentiation formulas and examples
The differentiation formulae are based on a set of principles that must be followed. Sum or difference rules, product rules, quotient rules, and chain rules are examples of such rules. Separation formulae are some of the most important differentiation formulas to know about. The following are only a handful of the more significant ones:
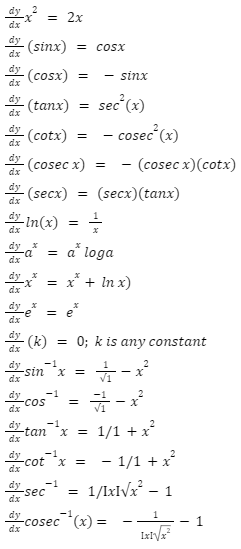
Linear and Non-Linear Functions
Under Calculus, functions are often divided into two types, which are as follows:
- Linear functions
- Non-linear functions
A linear function is a function that changes at a consistent pace across its domain. Because of this, the rate of change for the function as a whole is equal to that for the function at any given point.
In the case of non-linear functions, on the other hand, the rate of change of the function changes from point to point. The type of variation is determined by the nature of the function being considered.
The derivative of a function at a certain point is defined as the rate of change of that function at that particular moment in time.
Rules of differentiation
Sum and Difference Rule
According to the sum and difference rule, if the function f(x) is the sum or difference of two functions, say a(x) and b(x), the function’s derivative is:
If f(x) = a(x) + b(x) then,
f’(x) = a’(x)+ b’(x)
If f(x) = a(x) – b(x) then,
f’(x) = a’(x) – b’(x)
Product Rule
If a function f(x) is the product of two functions, say a(x) and b(x), the derivative of that function is:
If f(x) = a(x) * b(x) then,f’(x) = a’(x) * b(x) + a(x) * b’(x)
Chain Rule
how to differentiate quotient rule
If the function f(x) is the quotient of two functions, a(x)/b(x), then the derivative of the function is as follows, according to the quotient rule:
If f(x) = a(x)/b(x) then, f’(x) = a’(x) * b(x) – a(x) * b’(x) / (b(x))2
For this reason, according to the theory, for individual functions comprised of combinations of these classes that are differentiable by the sum, product, or quotient of two functions f(x) and g(x), whose derivative is known, the following essential requirements are given: (where a and b are constant).
D(af + bg) = aDf + bDg (sum); D(fg) = fDg + gDf (product); and D(f/g) = (gDf – fDg)/g2)
Notations
When a function is given by the notation y=f(x), the derivative is represented by the notations shown below.
D(y) or D[f(x)] This is referred to as Euler’s notation.
dy/dx This form is referred to as Leibniz’s notation.
F’(x) This is referred to as Lagrange’s notation.
It is the process of calculating the derivative of a function at any moment in time that is the definition of differentiation.
Conclusion
Differential equations are used extensively in research and engineering applications. It can be found in a wide range of technical applications, including as electromagnetic theory, signal processing, and computational fluid dynamics, among others. Analytical or numerical approaches are commonly used to solve these equations. So, if you want to be a master at differentiation, you must know all of the formulas and how they are obtained. Differentiation is defined as the pace at which one quantity changes in relation to another quantity. The rate of change in distance with respect to time is used to calculate the speed of a vehicle. The speed measured at each moment is not the same as the average speed determined in the previous step.
