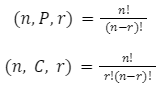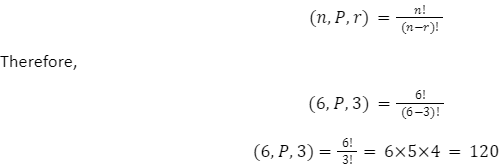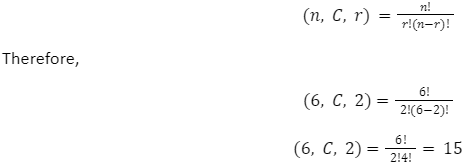Profile
Settings
Refer your friends
Sign out
Knowing the many contexts in which the notions of permutations and combinations are utilised can help you understand how they differ from one another. Combinations are used to group objects or to determine how many subgroups can be formed from the given collection of objects. Additionally, we use permutations to determine the amount of potential combinations of unrelated objects.
Finding the distinction between permutation & combination can be done with the aid of the permutation and combination formulas.
Permutation
A permutation is a list of the various configurations that can be created from the given set of items. Consider the letters P, 4, and $. These three characters can be combined to create a variety of passwords, including P4$, P$4, $4P, $P4, 4$P and 4P$. This is a straightforward illustration of how three characters can be used to create six different password permutations. Factorial of n divided by the factorial of difference of n & r equals the permutations of r things picked from n things.
Combination
Combinations are based entirely on grouping. Combinations can be used to determine how many different groups that can be created from the available items. Let’s use a straightforward example to try to comprehend this. The four children of a guy are Sam, Santa, John and Mary. If he is only permitted to bring three kids to the park at once, he might do so in one of the following ways:
Sam, Santa, John
Santa, Sam, Mary
Mary, Sam, John
John, Mary, Santa
These are the 4 possible combinations of three kids that can go to the park. As a result, the factorial of n would be the product of factorial of r & factorial of n divided by the combination of ‘r’ things from available ‘n’ things (n – r).
Difference Between Combinations and Permutations
Permutation | Combination |
When an order or sequence of arrangement is required, then permutations are used. | To determine the number of all the possible groups that can form, combinations are employed. |
For several types of items, permutations are required. | Combinations are utilized for comparable items. |
Permutation of two of the three provided items in a different way a, b, and c are ab, ba, cb, bc, ac, and ca. | Combining two of the three given items a, b, and c gives us ab, bc, and ca. |
nPr and nCr
The mathematical symbols for permutations and combinations—two crucial ideas in mathematics—are nPr and nCr. Although the goals of each of these notions are similar, they differ on a number of other fronts as well.
Differentiate Between Combinations and Permutations Examples
There are many uses for the permutation & the combination in daily life. Furthermore, probability can benefit from understanding permutations and combinations. The following list includes some examples of permutation & combination in use.
- The formula for permutations can be used to compute the various possible seating arrangements for important occasions or for official seating arrangements
- The permutation formula is used to determine the many password combinations that can be created from the provided numbers, symbols, and alphabets
- Knowing the various numbers of teams that can be formed makes it easier to form Teams from a wider number of prospective players. Combinations are helpful in determining the number of teams that could potentially emerge in this situation
- Additionally, the members of the various committees are chosen, and the combinations formula is used to determine the number of possible committee formations
Conclusion
Permutations can be used to determine how many distinct arrangements can be made using the provided items.
The combination can be used to determine how many distinct subgroups can be created from the given bigger set.
The number of permutation (arrangements) is always greater than the number of combination for the identical values of n and r.
