The derivative meaning of function in calculus is the mathematics of continuous change or the rate of change of a quantity concerning another. We can find the derivative at every point for a given function f in x, i.e., f(x). It simply means it is a function f concerning x. The function f changes the input into an output. If we take out the derivative of this function, then the function f will change to f’, df/dx, or f’ (x). As we perform different operations on numbers likewise, we can define algebra as function derivatives, such as sum, difference, product, and quotient.
Meaning of a Determinant
A determinant refers to an element that determines or identifies the value or nature of something.
- Every square matrix of order n can be associated with a real or complex number in mathematics. That real or complex number is called the determinant of square matrix A.
- Only square matrices can have determinants.
Properties of Determinants of Matrices
- Evaluation of matrices across any row or column turns out to be the same.
- If any two rows of a determinant are interchanged, the determinant’s value gets multiplied by -1.
- If all row or column elements are zeros, the determinant’s value shall be zero.
- The determinant of an Identity matrix (In) happens to be 1.
- The determinant of a triangular matrix, the diagonal matrix, is the product of the element of the principal diagonal.
- The determinant’s value remains unchanged if the rows and columns are interchanged. As such, det(A) = det(AT), where AT is the transpose of matrix A.
- If the multiplication of all the elements of a row (or column) of a determinant by some scalar number x takes place, the new determinant is x times the provided determinant. Therefore, If Y is an n-rowed square matrix while X is any scalar, then |YX| = Yn |X|.
- If two rows (or columns) happen to be identical, the determinant’s value is zero.
- In case, A and B be two matrices, then det(AB) = det(A)*det(B).
- In a determinant, if each element in any column or row involves the sum of two terms, its expression can be the sum of two determinants of the same order.
Differentiation of Determinants
In equations, the determinant is a price related to a rectangular matrix. It may be computed from entries of the matrix via means of a selected mathematics expression, proven below:
For a 2×2 matrix, [a b]
[c d]
the determinant will be; ad- bc
In the equation, the cofactor d, referred to as an adjunct, interprets a selected creation that helps compute each determinant of rectangular matrices and the inverse of rectangular matrices. The cofactor of the (i,j) access of a matrix, also called the (i,j) cofactor of a matrix, is the smallest of that access. The cofactor and access of a matrix is described as:
Cij= (-1)i+jMij
Dependents received through casting off barely one row and one column from rectangular matrices (main minors) are compelled for calculating matrix cofactors. Let A be an m× n matrix and k a number with 0<k≤m and k ≤ n. A k × k small of A is the determinant of a k×k matrix obtained from A by eliminating m−k rows and n−k sections.
Characteristics of Determinants
- Determinants are represented similar to a matrix but with a modulus sign.
- The first theorem shows how switching two rows in a matrix affects the determinant.
det I = 1;
- If any square matrix B with order n × n has a zero row or a zero column, then det(B) = 0.
- If C is upper-triangular or a lower-triangular matrix, then det(C) is the product of all its diagonal entries.
- If D is a square matrix and its row is multiplied by a constant k, the constant can be taken out of the determinant.
Rules for Operations on Determinants
To conduct column and row operations on determinants, use the following rules:
- If the columns and rows are swapped, the determinant’s value stays intact.
- The determinants sign changes if any two types or (two columns) are swapped.
- The determinant has a 0 value if any two rows or columns of a matrix are equal.
- The determinant is a sum of determinants if the row or column elements are expressed as the sum of elements.
- If elements of a row or column are added or subtracted with corresponding multiples of elements of another row or column, the value of the determinant remains unchanged.
Conclusion
Determinants, commonly categorised as first-order determinants, second-order determinants, and third-order determinants, provide a similar formula to find a solution to a system of n equations in n unknowns. This article discusses various formulas and methods of differentiation of determinants. Differentiation is finding out the rate of change of a parameter. The rate of change of a parameter is known as its derivative.

Binomial theorem for positive integral indices
According to the binomial theorem, the total number of terms in an expansion is always more than the index. Take, for example, an expansion of (a + b)n with n+1 terms and n as the index of the equation (a + b)n, where n is any positive integer.
The binomial theorem can be used to extend (x + y)n, where n is any rational number. Let’s look at the binomial theorem for positive integral indices.
The binomial theorem is a rule that can be used to enlarge any power of a binomial.

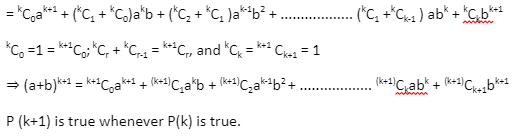
Therefore, P(n) is true for all positive integral values of n.
Properties of binomial theorem
- In the binomial expansion of (x+y)n, the number of coefficients is (n+1).
- In the expansion of (x+y)n, there are (n+1) terms.
- xn and yn are the first term and last term respectively.
- The powers of x decrease from n to 0 as the expansion advances, whereas the powers of y increase from 0 to n.
- The (r +1)th in the general term of of expansion is (x + y) n, which may be written as Tr+1=nCr xn-ryr.
- The coefficients of binomial expansion are organised into Pascal’s triangle.
- The nth term from the end of (x-y)n equals the (n-r+2)th term from the beginning in binomial expansion.
- The middle term in (x + y)n is (n/2)+1 if n is even; however, if n is odd, the middle terms are (n+1)/2 and (n+3)/2.
Coefficient of binomial theorem
The binomial coefficients are the figures associated with the variables x, y, in the expansion of (x +y)n. The binomial portions are represented as nC0, nC1, nC2. The binomial coefficients are attained through the Pascal triangle or by using the combinations formula.
Conclusion
The binomial expansion has more application than algebra II. In statistics, it is used to calculate the binomial distribution.
This allows statisticians to quantify the risk of a certain number of positive results in a set of trials.
Binomial expansion is also intriguing from a fine perspective as it allows mathematicians to gain insight into the properties of polynomials.
Binomial developments are used in numerous numerical and logical calculations, including kinematic and gravitational time enlargement, active energy, electric quadrupole post and determining the relativity factor gamma, to mention a few.
The number of terms in a binomial expansion of a binomial articulation raised to some power is another factor of the binomial development.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






