Onto Function is another name for Surjective function. When determining the inverse of a function, the concept of onto function is critical. To determine whether a function is onto, we need to know information about both sets involved. A type of function in which at least one element of the co-domain does not have a pre-image in the domain. Assume there are two sets, A (domain) and B (domain) (codomain)
An onto function is one whose image is the same as its codomain. An onto function’s range and codomain are also equal. An into function’s range will be a subset of the codomain. The range, however, will not be equal to the codomain. An into function’s elements are typically represented as an ordered pair of the form (input, output).
What are onto and into functions
Onto functions
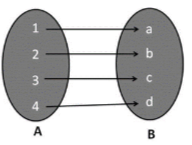
An onto function is one whose image is the same as its codomain. An onto function’s range and codomain are also equal. When every y codomain has at least one pre-image x domain, we can say that function is onto.
An onto function is a function f from set A to set B that exists for each B and has at least one an A such that f(a) = b. Because they are all mapped to some element of A, none of the elements are left out in the onto function.
Consider the following example:
A = {a1,a2,a3 } and B = {b1,b2 } then f : A→B.
into functions
An into function is a type of function that establishes a binary relationship between two sets such that each element of the first set (domain) is associated with exactly one element of the second set (codomain), and at least one element of the codomain is not associated with any element in the domain.
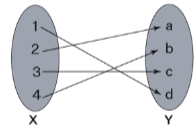
There will be one or more elements in set B that do not have a pre-image in set A for a function f: A →B to be an into function. In other words, not all elements of the codomain will be mapped to domain elements in an into function. As a result, an into function’s range will be a subset of the codomain, but the range and codomain will never be equal.
Example: Sets P = {1, 2, 3} and Q = {7, 8, 9, 10} are defined by the function f = (1, 7), (2, 9), (3, 8). Because element 10 of set Q lacks a pre-image in set P, this function is an into function.
Formulas of onto and into functions
Onto functions
There is a formula for calculating the number of onto functions that can be transferred from one set to another. We must ensure that all of the elements of B are used in the function from A to B.
If A has m elements and B has n elements, then using the formula, the total number of onto functions can be calculated.
nm–(n c 1)n-1m+(n C 2)(n-2m)……-1n-1(nC n-1)1m
It is important to note that this formula will only work if m ≥ n. However, if m < n, the number of onto functions will be 0 because it is impossible to use all of the elements of B.
Into functions
Total number of into function ={nPm , n≥m and 0, n<m
Differences of onto and into functions
Onto functions | Into functions |
Every element in the codomain will have at least one pre-image in the domain in an onto function. It is also referred to as subjective mapping. |
There will be at least one element in the codomain in an into function that does not have a domain pre-image. |
The following is an arrow diagram for an onto function: | The following is an arrow diagram for an into function: |
An onto function’s range and codomain are both equal. |
An into function’s range will be a subset of the codomain. The range, however, will not be equal to the codomain. |
Example:A = {1, 2, 3, 4}, B = {a, b, c} and f = {(1, b), (2, a), (3, c), (4, c)} |
Example: X = {a, b, c}, Y ={1, 2, 3, 4} and f = {(a, 1), (b, 2), (c, 3)} |
Conclusion
In this article we conclude that the distinction between the Into and Onto functions Each element of the output set y should be connected to the input set for Onto functions. For Into functions, on the other hand, there must be at least one element in the output set y that is not connected to the input set. A onto function has the same domain and range. After we have substituted the domain, the range of a function is the complete set of all possible resulting values of the dependent variable (y, usually). In layman’s terms, the range is the set of y-values that result from substituting all possible x-values.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out