Differences Between Intermediate Value Theorem and Squeeze Theorem

A valuable technique for examining the limit of a function at a certain point, the squeeze theorem can be used in situations where other methods (such as factoring or multiplying by the conjugate) fail. There are other names for this theorem, including the Sandwich Theorem and the Pinch Theorem, but it is most generally referred to as the Squeeze Theorem.

The intermediate value theorem is a continuous function theorem that deals with continuous functions. The intermediate value theorem is important in mathematics, and it is particularly important in functional analysis. This theorem illustrates the advantages of a function’s continuity in more detail.

The Squeeze Theorem

A valuable technique for examining the limit of a function at a certain point, the squeeze theorem can be used in situations where other methods (such as factoring or multiplying by the conjugate) fail. There are other names for this theorem, including the Sandwich Theorem and the Pinch Theorem, but it is most generally referred to as the Squeeze Theorem.

The Squeeze Theorem, also known as the Sandwich theorem, is a tool for determining the limits of trigonometric functions that have been supplied. The pinching theorem is another name for this particular theory. In calculus, as well as in mathematical analysis, the Sandwich theorem is frequently used to solve problems. This theorem is most likely used to determine the limit of a function by comparing the limits of two other functions whose limits are known or can be determined with certainty. Now, let’s have a look at the claim and proof of the Sandwich theorem.

In the following statement, consider three real functions such that f(x) ≤ g(x) ≤ h(x) for every x in the definition’s common domain of definition. If there is a real number a, and if

xaf(x) = l = xa h(x)

then

xag(x) = l

Intermediate Value Theorem

Suppose “f” is a continuous function over the closed interval [a, b], and its domain contains the values f(a) and f(b) at the interval’s ends, then the function takes any value between the values f(a) and f(b) at any point within the interval, according to the intermediate value theorem. This theorem is explained in two ways: first, as follows:

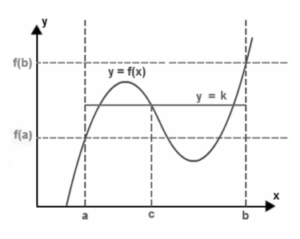
Statement 01:

If k is a number that falls between f(a) and f(b), then

In either case, f(a) < k < f(b) or f(a) > k > f(b)

In this case, there must be at least one number in the range from (a to b) called c. This number must be such that the value of f(c) = k.

Statement 02:

The set of images of a function in the range [a, b], which includes [f(a), f(b)] or [f(b), f(a)], i.e. either f([a, b]) ⊇ [f(a), f(b)] or f([a, b]) ⊇ [f(b), f(a)]

Explanation of the Theorem:

The statement of the intermediate value theorem appears to be difficult to comprehend. However, it is possible to understand it in simpler terms. Assuming the above picture has a continuous function f with endpoints a and b, the heights of the points “a” and “b” would be denoted by the letters “f(a)” and “f(b), respectively.

If we choose a height k between these heights f(a) and f(b), then according to this theory, this line must cross the function f at some point (say c), and this point must be located between the heights a and b, as shown in the diagram.

Bolzano’s theorem is an intermediate value theorem that holds if c = 0. It is also known as Bolzano’s theorem.

Difference

This is a rather straightforward formula because it essentially states that, given an infinitely long continuous function with a domain of [a, b], and “m” is some value BETWEEN f(a) and f(b), then there exists some positive integer c inside the interval such that f(c) = m.

If we ignore limitations for a moment, let us consider the following: if at some point in time and is equal to g(x), and at some point in time L is equal to h(x), then at some point an is equal to g(a) = h(a) = L, then f(a) = L. I mean, it’s self-explanatory, right? It has to happen. Because it’s not always clear whether g, f, and h exist at x = a the right definition makes use of bounds to clarify the situation.

Conclusion

Because it demonstrates that something exists but does not demonstrate how to find that entity, the intermediate value theorem is sometimes known as an existence theorem. As a result, the intermediate value theorem is frequently employed in proofs. It is most commonly used to evaluate challenging limitations, and it is used to bring up inequalities concerning boundaries through the use of imagination.