Differences between Intermediate Value Theorem and Extreme Value Theorem

The intermediate value theorem is a continuous function theorem that deals with continuous functions. The intermediate value theorem is important in mathematics, and it is particularly important in functional analysis. This theorem illustrates the advantages of a function’s continuity in more detail. In mathematics, the two most important examples of this theorem are frequently employed in many applications. 

Intermediate Value Theorem Statement: 

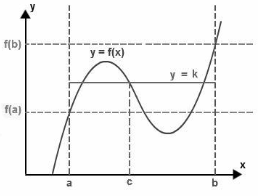
Suppose “f” is a continuous function over the closed interval [a, b], and its domain contains the values f(a) and f(b) at the interval’s ends, then the function takes any value between the values f(a) and f(b) at any point within the interval, according to the intermediate value theorem. This theorem is explained in two ways: first, as follows: 

Statement 1: 

If k is a number that falls between f(a) and f(b), then 

either f(a) < k < f(b) or f(a) > k > f(b) 

There exists at least one number c between a and b, that is, c ∈ (a,b) in a way that the function f(c) = k is satisfied. 

Statement 2: 

The set of images of function in interval [a, b], containing [f(a), f(b)] or [f(b), f(a)], i.e.

Either f([a, b]) ⊇ [f(a), f(b)] or f([a, b]) ⊇ [f(b), f(a)]

Theorem Explanation: 

The statement of the intermediate value theorem appears to be difficult to comprehend. However, it is possible to understand it in simpler terms. Assuming the above picture has a continuous function f with endpoints a and b, the heights of the points “a” and “b” would be denoted by the letters “f(a)” and “f(b), respectively.

If we choose a height k between these heights f(a) and f(b), then according to this theory, this line must cross the function f at some point (say c), and this point must be located between the heights a and b, as shown in the diagram.

Bolzano’s theorem is an intermediate value theorem that holds if c = 0. It is also known as Bolzano’s theorem. 

Intermediate Theorem proof: 

We will prove the first case of the first statement of the intermediate value theorem because the proof of the second case is quite similar to the proof of the first case.

In order to prove this theorem, we will make use of the condition of completeness of real numbers. The following is the proof of the statement “f(a) < k < f(b)”:

Take for example, the assumption that A is the set of all the values of x in the range [a, b], such that f(x) is less than or equal to k.

Because it contains the element “a” and because it is bounded above by the value “b,” A is assumed to be a non-empty set in this case.

According to the completeness property, we can say that “c” is the lowest number that is either higher than or equal to each element of A, and that this is the case. As a result, we can state that f(c) = k. 

Given that f is continuous. Then let us consider a ε > 0, there exists “a δ > 0” such that

| f(x) – f(c) | < ε for every | x – c | < δ. This gives us

f(x) – ε < f(c) < f(x) + ε

For each x lying within c – δ and c + δ. So, we have values of x lying between c and c -δ, contained in A, such that :

f(c) < (f(x) + ε) ≤ (k + ε) ——– (1)

Similarly, values of x between c and c + δ that are not contained in A, such that

f(c) > (f(x) – ε) > (k – ε) ——–(2)

Combining both the inequality relations, obtain

K – ε < f(c) < k + ε

For every ε > 0

Hence, the theorem is proved.

Extreme Value Theorem: 

On specific intervals, critical points are useful in determining the feasible maximum and lowest values of a function, which is an important application of critical points. According to specific conditions, the Extreme Value Theorem assures the existence of a maximum and a minimum value for a function. The following is stated in the document: 

• If a function f(x) is continuous on a closed interval [ a, b], then f(x) has both a maximum and minimum value on [ a, b]. 

First, it is necessary to prove that the function is continuous on the closed interval before proceeding with application of the Extreme Value Theorem. The following step is to identify all critical points within the specified interval and to evaluate the function at each of these critical points as well as at the beginning and ending points of the supplied interval. The maximum value of the function is represented by the greatest function value from the previous phase, and the minimum value of the function is represented by the smallest function value from the previous step. 

Proving the Theorems: 

We’ll take a look at the proof for the upper bound and the maximum of f before moving on. By applying these results to the function -f, it is possible to demonstrate the presence of the lower bound as well as the result for the minimum of f. Also keep in mind that everything in the proof is done in the context of the actual numbers.

Our first proof is the boundedness theorem, which is a step in the proof of the extreme value theorem. We then prove the boundedness inequality. The following are the fundamental steps involved in the proof of the extreme value theorem: 

• Demonstrate that the boundedness theorem holds
• Find a sequence in which the picture of the series converges to the supremum of f
• Identify a subsequence that converges to a point in the domain and demonstrate that it exists
• Show that the image of the subsequence converges to the image of the supremum by utilising continuity 

Conclusion: 

A function that is continuous on an interval [ a, b ] takes on all (intermediate) values between its extremes, according to the Intermediate Value Theorem (IVT). The Extreme Value Theorem (EVT) states that functions that are continuous on [ a, b ] reach their extreme values when they reach their extreme values.