Like differential calculus, integral calculus is an important part of calculus. In differential calculus, we investigate the relationship between two quantities such as distance and time. The rate of change between two variables is commonly used in this relationship.
The inverse process of the relationship between two quantities is used in integral calculus. Integration, anti-differentiation, or anti-derivative are terms used to describe this process. The most common use of integral calculus is to calculate a shape’s area or volume. The Greek mathematicians Archimedes (287 BC – 212 BC) and Eudoxus (410 BC – 347 BC) created the informal notions in ancient times. They constructed approximate areas for various geometric forms, and Chinese mathematician Liu Hui used these basic methods to find the area of a circle in the third century. In the seventeenth century, John Kepler refined some key principles in astronomical investigations to determine the area of a sector and an ellipse. Isaac Newton and Gottfried Leibniz formalised the concept of integral calculus by developing basic concepts for calculating area and volume.
Different topics such as the area of various geometric shapes, the area under the curve utilising the definite integral, the indefinite integral, and numerous practical applications are encountered in integral calculus. We also come across the “Fundamental Theorem of Calculus,” which is the most important theorem in calculus. This theorem builds on the idea that differentiation and integration are diametrically opposed procedures.
Definition of Integral:
An integral is a mathematical concept that describes how infinitesimal data can result in displacement, area, volume, and other concepts. The process of locating integrals is known as integration. Integration, like differentiation, is a fundamental, essential operation of calculus that can be used to answer issues in maths and physics involving the area of an arbitrary form, the length of a curve and the volume of a solid.
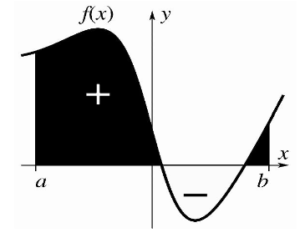
The signed area of the region bordered by a
function’s graph can be used to indicate its
definite integral.
The integrals listed below are known as definite integrals, and they are defined as the signed area of the plane region enclosed by the graph of a given function between two points in the real line. Positive areas are those above the plane’s horizontal axis, whereas negative areas are those below. Integrals refer to antiderivatives, or functions whose derivative is the specified function. In this case, they are known as indefinite integrals. The fundamental theorem of calculus links definite integrals to differentiation and provides a method for determining a function’s definite integral when its antiderivative is known.
Definition of Definite Integrals:
A continuous function f(x) on the closed interval [a, b) is used to build the definite integral definition. The provided interval is divided into “ n” subintervals that can be assumed to be of equal length (∆x), while this is not required. In each subinterval, an arbitrary domain value, xᵢ is picked, and its subsequent function value, f(xᵢ) is calculated. The sum of these “ n” products is obtained by multiplying each function value by the length of the relevant subinterval. This total is known as a Riemann sum, and it can be positive, negative, or zero depending on how the function behaves on the closed interval. If f(x) > 0 on [a, b], for example, the Riemann sum is a positive real number. If f(x) is less than zero on [a, b], the Riemann sum will be negative. On [a, b], the Riemann sum of the function f(x) is given as
S₊ = f(x₁)∆x+ f(x₂)∆x+f(x₃)∆x+…+f(xₙ)∆x or Sₙ= ∑ⁿᵢ₌₁f(x)ᵢ∆x
As a result, a “sum of n products” can be conceived of as a Riemann sum.
Difference Between Definite and Indefinite Integrals:
Calculus is one of the most significant fields of mathematics. Calculus is a systematic method of solving issues that usually involves using integrals and derivatives to identify properties or values of functions. Differentiation and integration are the fundamental concepts of calculus. The two conceptions are the polar opposites of one another. Differential is the inverse of integral, while differential is the inverse of differential. Integrals are classified as definite or indefinite based on the consequences they produce.
The difference between definite and indefinite integral solutions is that in definite integral, we know we have upper and lower bounds, so we just get a number after integrating the given function, whereas in indefinite integral, we simply integrate a function and add an arbitrary constant. We can get the value of that arbitrary constant and thus a suitable function by using initial conditions.
The only thing that separates them is a constant. When the limits are constant, we receive the constant value as described above and in the suggestion; if the limits are not constant, we get the function as described in the indefinite integral but without the arbitrary constant. We can also say that in a definite integral, we just get a number after the limits, so we can call it definite, but in an indefinite integral, we don’t get any definite number in our solution and thus get the variables, so we can call it an indefinite integral, and without any given conditions, we can’t get the value of an arbitrary constant either.
Concept of Integral and Definite Integrals:
A formal calculation of area beneath a function using infinitesimal slivers or stripes of the region is known as a definite integral. Integrals can be used to indicate the area of a region (signed), the accumulated value of a function changing over time, or the quantity of an item given its density. The contemporary notation is based on Liebniz’s notes, and the definite integral is represented with a real-valued function f and real values a<b.
b∫ₐ f(x) dx
This value reflects the signed area between the function f, the x-axis, and the lines x = a and x = b; positive area is above the x-axis, while negative area is below the x-axis.
The indefinite version of a definite integral acts as a partial inverse to differentiation. A definite integral attempts to “undo” what differentiation measures: incremental changes in a function. As a result, integrals emphasise aggregation above change.
In economics, finance, science, and engineering, definite integrals are useful. For example, marginal cost becomes cost, income rates become total income, velocity becomes distance, and density becomes volume. Definite integrals are also used to calculate arc length, volumes, and surface areas, among other functions. In generalised situations, definite integrals include line integrals, surface integrals, and contour integrals.
Conclusion:
Integrals are used in both science and mathematics. Integral is used in mathematics to find the area under a curve, the area between two curves, the centre of mass of a body, and so on. Integrals are used in science (particularly in physics) to compute the Centre of Gravity, Mass, Momentum, Work done, Kinetic Energy, Velocity, Trajectory, and Thrust.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






