When the process of integration is completed, the values of the function discovered are called integrals. Integration is the term used to describe the process of obtaining f(x) from f’(x). Integrals are used to assign numbers to functions in a way that describes displacement and motion difficulties, area and volume problems, and other problems that come as a result of integrating all of the little data into a single large number. We can find the function f by taking the derivative f’ of the function f and solving for f. In this case, the function f is referred to as the antiderivative or integral of f’. 

Types of Integrals: 

It is necessary to apply integral calculus in order to solve the problems of the following types. 

• The difficulty of determining the derivative of a function when just the function’s name is known. 
• A second challenge is the problem of determining the area enclosed by the graph of a function under specified conditions. 

As a result, the Integral calculus can be separated into two categories: 

1. Definite integrals

2. Indefinite integrals 

Definite Integrals: 

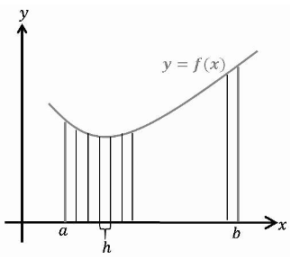
It is the area under a curve between two set limits that is known as a definite integral. The definite integral of a function f(x) defined with reference to the x-axis is represented by the expression b∫a f(x)dx, where an is the lower limit and b is the upper limit. If we want to find the area under a curve between two points, we divide the area into rectangles and add the sums of the rectangles together. The greater the number of rectangles used, the more accurate the area calculation is made. Consequently, we divide the area into an unlimited number of rectangles, each of equal (very small) size, and then add the totals of all of the rectangles. Definite integrals are based on this fundamental idea, which is explained more below.

Definite Integral formula: 

When determining the value of a definite integral, definite integral formulas are utilised. We have two formulas for evaluating a definite integral, which are discussed more below. It is known as the “definite integral as a limit sum” in the first formula, and it is known as the “basic theorem of calculus” in the second formula, respectively. 

• ^b∫_a f(x)dx = lim_n→∞∑ ⁿr=1hf(a+rh) where h = b-a/n 
• ^b∫_a f(x)dx = F(b)-F(a) where F’(x) = f(x) 

Definite Integral as limit sum: 

As previously stated, we can express the area under a curve between two given limits as the sum of an unlimited number of rectangles, which is what we did in the previous section. This concept can be applied in order to evaluate the value of a definite integral, for example, b∫a f(x)dx. To do so, we divide the area under the curve into many rectangles, with each rectangle being divided into an infinite number of subintervals. As a result, the definite integral as a limit sum formula is as follows: 

^b∫_a f(x)dx = lim_n→∞∑ ⁿr=1 hf(a+rh) 

The length of each subinterval is represented by the expression h = b-a/n. 

Definite Integral formula using FTC: 

The fundamental theorem of calculus can be used to assess a definite integral b∫a f(x)dx, which is defined as (FTC). This is the quickest and most straightforward method of assessing a definite integral. This formula instructs you to first determine the antiderivative (indefinite integral) of f(x) (and represent it as F(x)), then substitute the upper limit first, followed by the lower limit one by one, and finally subtract the results in the order they were obtained. i.e., 

^b∫_a f(x)dx = F(b)-F(a), where F’(x) = f(x) 

Indefinite Integrals: 

An indeterminate integral is an integral that does not have any upper or lower bounds and so has no upper or lower bounds.

According to mathematics, if F(x) is any anti-derivative of f(x), then the greatest generic anti-derivative of f(x) is referred to as an indefinite integral and indicated by the symbol 

∫f(x) dx = F(x) + C 

The anti derivatives and integrals of the functions are not distinct from one another. Every one of certain functions has an infinite number of antiderivatives, which may be derived by selecting C at random from the set of all possible real numbers. As a result, C is commonly referred to as an arbitrary constant in the literature. Different antiderivatives (or integrals) of the following function can be obtained by varying the value of the parameter C. 

Indefinite Properties: 

• Differentiation and integration are two processes that are diametrically opposed to one another. 

• Two indefinite integrals with the same derivative result in the same family of curves, and as a result, they are equal in this regard. 
• The integral of the sum of two functions is equal to the sum of the integrals of the two functions that are given as inputs to the function.

Conclusion: 

A function that practises the antiderivative of another function is referred to as an indefinite integral. It can be represented visually as an integral symbol, followed by a function, and finally a dx at the conclusion. The indefinite integral is an easier way to denote acquiring the antiderivative. In some ways, the indefinite integral and the definite integral are the same thing, but they are not the same.