Determinant of 4 x4 matrix

According to a particular process, the sum of products of the elements of a square matrix and their cofactors generates determinants, which are scalar values. They help find the adjoint, or inverse, of a matrix. This methodology must also be utilized to solve linear equations using the matrix inversion method. Calculating determinants helps remember the cross-product of two vectors much easier. In matrices, the determinants are the form of scaling factor. They can be compared to matrices that grow and contract in functions. Determinants take in a square matrix as input and output a single number. Definition of Determinants:

Consider a matrix C = [cij]

A determinant of order n x n can be defined as a scalar value that is either real or complex, where

Cij is the (i,j) the element of given matrix C. The determinant can be written as det(C) or |C|; instead of using square brackets, the determinant is written by taking the grid of integers and putting them inside the absolute-value bars.

Determinant of 4×4 matrix:

The determinant of any 4×4 matrix is a one-of-a-kind integer evaluated using a specific formula. It is a square matrix if the given matrix order is n x n. As a result, the 4×4 is a square matrix with four rows and four columns. The determinant of matrix A is represented as |A| if A is a square matrix.

We’ll use the same easy method we use to calculate the determinant of a 3×3 matrix to find the determinant of a 4×4 matrix.

Calculating a 4×4 Matrix’s Determinant

Consider the following 4×4 square matrix or a square matrix of order 4×4; when determining the determinant of a 4×4 matrix, keep the following changes in mind:

 B =  

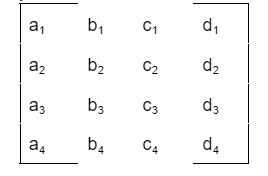
Steps: 

• plus a1 times the 3×3 matrix’s determinant obtained by deleting the row and column containing a1

•  minus b1 times the 3×3 matrix’s determinant obtained by deleting the row and column containing b1 

• plus c1 times the 3×3 matrix’s determinant obtained by deleting the row and column containing c1

• minus d1 times the determinant of the 3×3 matrix obtained by deleting the row and column containing d1

Rules for implying operations on determinant:

1-The determinant’s value remains unchanged if the rows and columns are swapped.

2-The determinant’s sign changes if any two rows or (two columns) are swapped.

3-If any two rows or columns of a matrix are equal, the determinant has zero value.

4-The determinant’s value is multiplied by the constant when each element of a row or column is multiplied by the constant.

5-If the constituents of a row or column are expressed as a sum of elements, the determinant can be expressed as a sum of determinants.

6-When the elements of one row or column are added or subtracted with the matching multiples of elements from another row or column, the determinant’s value remains unchanged.

Important Determinants Notes:

Here’s a rundown of some key elements to keep in mind when studying determinants.

Determinants can be thought of as functions that take a square matrix as input and output a single value.

On both sides, the square matrix is the equal number of rows and columns.

The determinant of the simplest square matrix of order 1×1 matrix, which only has one number, is the integer itself.

Conclusion:

The determinant is a scalar variable in mathematics that is a function of the entries of a square matrix. It allows us to characterize some of the matrix’s attributes as well as the linear map that the matrix represents. The determinant is nonzero if and only if the matrix is invertible and the linear map that the matrix represents is an isomorphism. Det(A), det A, or |A| is the determinant of a matrix A. The determinant of a 4×4 matrix is a one-of-a-kind integer that can only be calculated using a specific formula. It is a square matrix if the given matrix order is of n x n. So, a square matrix with four rows and four columns is 4×4. The determinant of the matrix A is represented as |A| if A is a square matrix.

To find the determinant  we’ll utilize the standard way; there’s a formula for finding the determinant of a 4×4 matrix that we usually use to get the determinant of a 3×3 matrix.