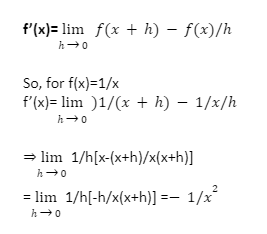Introduction
What are the derivatives of polynomial?
Derivatives determine the rate by which a parameter changes with time. In real life, we are required to evaluate the rate of change to know when a reservoir will overflow by knowing the water depth at different times. The Astroscientists determine the velocity they need to shoot the satellite from the rocket. They do so by knowing the rocket’s height with time.
In the language of mathematics, we use the derivative to find a function’s maxima or minima and slope. We can see whether the function decreases or increases over time by determining its rate of change with regard to a variable. In this derivatives of polynomial study material, we shall discuss the core of derivatives of the polynomial.
Basic Rules of Derivative
- Power rule
f’ (xn)=n.xn-1
- Constant multiple Rule
(cf)’= c’f’ where c=constant
Let f and g be two functions with their derivatives defined in a common domain. So, we can apply the basic rules of differentiation on such as:
- Sum rule
The addition rule of derivatives states that the derivative of the sum of two functions is the sum of the functions’ derivatives.
d/dx [f(x)+g(x)]
= d/dx f(x)+d/dx g(x)
- Difference rule
The subtraction rule of derivatives states that the derivative of difference of the two functions is the difference of each derivative’s derivative
d/dx [f(x)-g(x)]
= d/dx f(x)-d/dx g(x)
- The product of two derivatives/ Product rule
Dot Product of two functions’ derivatives is equal to the product rule of both functions
d/dx [f(x).g(x)]
= d/dx f(x).g(x)+d/dx f(x).g(x)
- The quotient of two derivatives/ Quotient rule
The quotient of two functions’ derivative is equal to the quotient rule, givenDr0
d/dx(f(x)/g(x))= d/dx f(x).g(x)-f(x). d/dx g(x)/(g(x))2
Derivatives of Polynomial
The theorem of derivatives of polynomial states that, if:
f(x)= anxn+ an-1xn-1+…+a1x+a0 is a polynomial function, where ais are real numbers and ans0
Then, we can get the derivative function as:
df(x)/ dx= nanxn-1+ (n-1) an-1xn-2+…+2a2x +a1
Proof for (xn)’=n.xn-1
We can determine the derivatives of polynomial starting from a constant value of the function and ending with xn
- f(x)=y=constant, the derivative is zero
d/dx(c)=h0(f(x+h)-f(x)) /h
=h0c-c/h
=0
- f(x)=y=x for the completeness and prove the derivative is 1
dy/dx= dx/dx=h0f(x+h)-x/h
= (x+h)-x/h
h/h =1
So, for y=f(x)=xn where n is a positive integer
- c) Expanding f(x+h)=(x+h)nusing the binomial theorem
(x+h)n=xn+nxn-1h+(n(n-1)/2)xn-2h2+…+nxhn-1+hn
So, differentiating d/dx xn=h0(xn+nxn-1h+(n(n-1)/2)xn-2h2+…+nxhn-1+hn)-xn
=h0(nxn-1…+hn-1)= nxn-1
Examples
- Let’s resolve the following polynomial: f(x)=x6+2×4+3×2+2
Ans: f’(x)= (x6+2×4+3×2+2)’
So, using the constant multiple and power rule, we get
=6×5+8×3+6x
- Find the derivative of f(x)=(x3)(2x)
Ans: Using Product rule which is
d/dx [f(x).g(x)] = d/dx f(x).g(x)+d/dx f(x).g(x), we get
f’(x)= (x3)(2x)’+(x3)'(2x)
f’(x)= 2×3+6×3=8×3
- Find the derivative of x2+1/x+2
Ans: Since, as per the quotient rule,
d/dx(f(x)/g(x))= d/dx f(x).g(x)-f(x) d/dxg(x)/(g(x))2
f’(x)=(x+2)(x2+1)’ – (x2+1)(x+2)’ /(x+2)2
= 2×2+4x-x2-1/(x+2)2
Thus, we get;
x2+4x-1/x2+4x+4
Conclusion
Differentiation for polynomials involves the use of basic rules of differentiation. In this guide, we have demonstrated how we can apply the constant multiple rule and power rule to extend our range of differentiation to complex polynomials. In addition, we discussed basic derivatives used to find polynomial derivatives, including the sum rule, difference rule, product rule, and quotient rule. Also, we studied how to determine polynomial derivatives by solving different mathematical problems.
We also performed derivation to prove the derivatives of polynomials from scratch by first taking the function as constant and then ending with a derivative for xn. For the xn derivative, we also learned the significance of the binomial theorem.
Now that you have gone through the study material notes on derivatives of polynomials, it’s time to brush up on the concepts and try out some FAQs for derivatives of the polynomial.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out