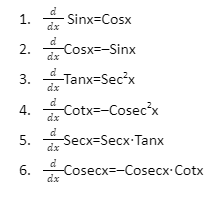Profile
Settings
Refer your friends
Sign out
Derivatives are used in mathematics to solve various problems related to the graph. In a graph, with the function given, it is useful to measure the slope at some particular point. Thus, we can define derivatives as the ratio of the change in the value of the given function to the change in the value of the independent variable.
The below sections present an overview of the derivative formula and the rules of derivatives.
Definition of Derivative formula
In calculus, we can write the derivative formula for the variable ‘x’ having an exponent ‘n’ (where the exponent ‘n’ can be an integer or a rational fraction) as follows.
ddx.xn= n.xn−1
Derivation of Derivative Formula
Let there be a function f(x) with a domain containing x0 (about some point) as an open interval. Thus, by differentiating f(x) at the point x0 we get the derivative which can be represented by using the formula as.
f'(x)= limΔx→0 Δy/Δx
⇒ f'(x)= limΔx→0 [f((x)0+Δx)−f((x)0]/Δx
let the function y = f(x) derivatives be f′(x) or y′(x)
We can present the derivative of the function by using the well-known Leibniz’s notation:
y = f(x) as df(x)/dx, i.e., dy/dx
Basic rules to find derivatives
Constant rule
According to the constant rule of derivatives, since a constant function is a horizontal line, the slope is zero or the rate of change of a constant function. Thus, we can say the derivative of the constant function is always taken as zero.
ddx (c)=0.
Power Rule
Power Rule says that you have to take the exponent and multiply it with the coefficient and then decrease that exponent by 1.
d/dx(x2) = 2x and d/dx(x1/2) = ½ x-1/2
Sum rule
The derivative of the sum of a function f and a function g is the same as the sum of the derivative of f and the derivative of g.
d/dx(f(x)+g(x))=d/dx(f(x))+d/dx(g(x))
Difference rule
The derivative of the difference of a function f and a function g is the same as the difference of the derivative of f and the derivative of g :
d/dx(f(x)−g(x))=d/dx(f(x))−d/dx(g(x))
Constant Multiple rules
The derivative of a constant c multiplied by a function f is the same as the constant multiplied by the derivative:
d/dx(kf(x))=kd/dx(f(x))
Product rule
The Product rule states that the derivative of the first function times the second function plus the derivative of the second function times the first function is the derivative of a product of two functions.
d/dx(f(x)g(x))=d/dx(f(x))⋅g(x)+d/dx(g(x))⋅f(x)
Quotient rule
Quotient rule is used to find the derivation of a function that has the two differentiable functions in a ratio.
d/dx(f(x)g(x)) = [d/dx(f(x))⋅g(x)−d/dx(g(x))⋅f(x)](g(x))2
List of the derivatives formula of different functions
Derivative Formula of Logarithm Functions:
d/dx ln x=1/x
d/dx logax=1x ln a
d/ dx ln f(x)=1fx ddxf(x)
d/dx loga f(x)= 1fxln a d/dxf(x)
Derivative Formula of Exponential Functions:
d/dx ex=ex
d/dx ef(x) =ef(x) ddx f(x)
d/dx ax=ax ln a
d/dx af(x) = af(x) ln addxf(x)
d/dx xx=xx(1+ln x)
Derivative Formula of Trigonometric Functions:
d/dx Sinx = Cosx
d/dxCosx = –Sinx
d/dxTanx = Sec2x
d/dxCotx = –Cosec2x
d/dxSecx = Secx⋅Tanx
d/dxCosecx = –Cosecx⋅Cotx
Derivative Formula of Hyperbolic Functions:
d/dx Sinhx=Coshx
d/dx Coshx=Sinhx
d/dxTanhx=Sech2x
d/dxCothx=−Cosech2x
d/dxSechx=−Sechx⋅Tanhx
d/dx Cosechx=−Cosechx⋅Cothx
Derivative Formula of Inverse Trigonometric Functions:
d/dxSin–1x = 1/√(1–x2), –1<x<1
d/dxCos–1x = –1/√1–x2, –1<x<1
d/dxTan–1x = 1/(1+x2)
d/dxCot–1x = –1/1+x2
d/dxSec–1x = 1/x√(x2–1), |x|>1
d/dxCosec–1x = –1/x√(x2–1), |x|>1
Derivative Formula of Inverse Hyperbolic Functions:
d/dxSinh–1 x=1/√1+x2
ddxCosh–1 x=1/√x2–1
d/dxTanh–1 x=1/1–x2, |x|<1
d/dxCoth–1 x=1/x2–1, |x|>1
d/dxSech–1 x=–1/x √1–x2, 0<x<1
d/dxCosech–1 x=–1/x√1+x2, x>0
Derivative Formula Questions and Solutions
1: What is ddxx3?
Solution:
We apply the formula ddx (xn)=n xn−1
Here, n=3.
So, the answer for the above equation is 3x²
2: What is the derivative of f(x) = 25 ?
Solution:
Since the function is constant, its derivative will be zero.
In other words, f’(x) = 0
Conclusion
Thus, we can conclude that derivatives are an important part of calculus calculations. The different derivative formulas of hyperbolic function, log function, inverse hyperbolic function, exponential function, trigonometric function, and inverse trigonometric function need to be learned to differentiate the derivative. Derivatives are useful to find the slope of the line or curve at any point on a graph.
