A triangle is a three-sided polygon that lies within a two-dimensional plane. This three-sided polygon is made up of three lines that meet end to end, to make an enclosed figure of which the sum of internal angles is 180°. The point where any of the two sides meet makes an angle, and therefore, a triangle, as its name states, has three angles. All the properties related to a triangle are dependent upon the length of its sides and the angles of the triangle. It is these two that greatly affect the solution of a triangle.
Triangle is a Three-sided Polygon
Triangles can be classified on the following two bases:
- Based on the measure of their sides
- Based on the degree measure of their angles.
Types of Triangles Based on the Length of Their Sides
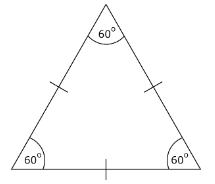
Equilateral Triangle
An equilateral triangle is the type of triangle for which each side of it will carry the same particular measure in terms of length. Each of the three angles inside an equilateral triangle has a value of 60°.
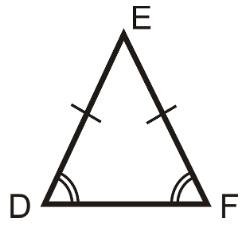
Isosceles Triangle
In an isosceles triangle, two of its sides have the same measure for their length. And, the angles opposite to the equal sides of this triangle also happen to be equal.
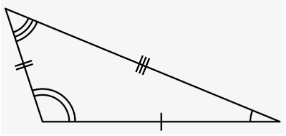
Scalene Triangle
This is the type of triangle in which each side carries a different length measure for it. And, none of the internal angels within the said triangle is of the same measure either.
Types of Triangles Based on the Measure of Their Angles
Acute-angled Triangle
An acute-angled triangle is the type of triangle in which all the internal angles are less than 90°.
Right-angled Triangle
This is the type of triangle in which one of the internal angles happens to be right-angled or of 90°.
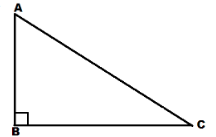
Obtuse-angled Triangle
A triangle that has one angle greater than 90° and has other two angles to be acute, is called an obtuse triangle.
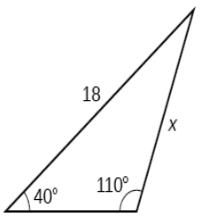
Sum of the Internal Angles
Internal Angles of the Triangle
No matter the type of triangle that it might turn out to be, equilateral, isosceles, scalene, acute, obtuse or right-angled, the sum of internal angles of a triangle is always 180°. Any polygon that is made up of three sides will always have an internal angle total of 180°.
It is to be kept in mind that two angles in a triangle are always acute, the last angle can be an acute, obtuse or right angle, depending on the angle sum property of the triangle. Hence, it is possible to calculate the third angle of a triangle if two of its angles are already known to us.
External Angles of a Triangle
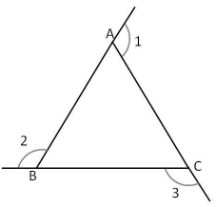
∠1 + ∠2 + ∠3 = 360°
The sum of internal angles of a triangle is 180°. On the other hand, the sum of the external angles of a three-sided polygon happens to be 360°. To find one of the external angles of a triangle, the internal angle of the triangle adjacent to it is to be subtracted from 180°. That outcome will be the measure of one of the external angles for that figure. By repeating this process three times, all the external angles of the triangle can be found.
As the external angle and the internal angle adjacent to it are supplementary, it is possible to find that angle out using opposite two angles.
Triangle is a Measure of 180 Degrees
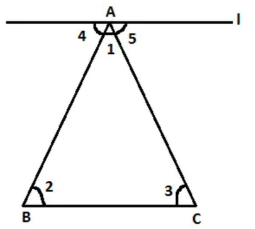
To prove that the sum of internal angles of a triangle is 180°.
Let there be a triangle ∆ABC. Consider there to be a line ‘l’ parallel to AB.
Now from the above-drawn figure, it can be derived that;
∠4 = ∠2 [ ••• Alternate Angles]
∠5 = ∠3 [ ••• Alternate Angles]
Utilising both of the above-mentioned equations:
∠4 + ∠5 = ∠2 + ∠3
Adding ∠1 on both the sides of this equation;
∠4 + ∠5 + ∠1 = ∠2 + ∠3 + ∠1
As the line ‘l’ is straight, the angle over a straight line is 180°.
Therefore,
∠1 + ∠2 + ∠3 = 180°
Conclusion
To calculate all the functions and properties that are related to a triangle, it is needed for us to be aware of the characteristics of a triangle. And on the bases of those characteristics, triangles are classified into different types. Each type of triangle has its own set of properties based on the linear characteristics related to that triangle. So, understanding such factors is much necessary to be able to completely grasp the mathematical concept of triangles.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






