Watch Free Classes

They are named after Augustus De Morgan , a British mathematician in the 19th century. The set of all those elements which are either in A or in B is the union of two sets A and B.

In other we can say that the complement of the intersection of two sets A and B is equal to the union of their separate complements.

But the our focus on the de morgan’s law on differences in set theory

Further in this article we will do the proof of this law as well.

And also take some questions related to this topic to understand this more easily and fast.

STATEMENT OF DE MORGAN’S LAW THEOREM IN SET THEORY

Let two sets be A and B and their complements  be A’ And B’ .

First law of De morgan’s says that the union of complement of the two sets A and B is equal to the intersection of their separate complements.

(A∪B)’=A’∩B’

Second law of De morgan’s  says that the complement of the intersection of two sets A and B is equal to the union of their separate complements.

(A∩B)’ = A’ B’

DE MORGAN’S LAW PROOF IN SET THEORY

FIRST LAW OF DE MORGAN’S LAW:

Let X=(A∪B)’  and Y= A’∩B’

Let m be an arbitrary element of X so , m∈X

Which means  m (A∪B)’

m (A∪B)

m A and m ∈B

m ∈A’  and m ∈B’

m ∈Y

hence, X ∈Y  ………………….(i)

now let n be the arbitrary element of Y so , n ∈Y

which means n A’∩B’

n A’ and n ∈B’

n ∈A and n ∈B

n (A∪B)

n (A∪B)’

n ∈Y

Y∈X …………………………(ii)

From equation (i) and (ii)

X =Y

(A∪B)’=A’∩B’

SECOND LAW OF DE MORGAN’S LAW:

Let X =(A∩B)’ and Y= A’∪B’

Let m be an arbitrary element of X so , m X

Which means m (A∩B)’

m ∈A and m ∈B 

 m ∈A’ and m∈B’

m A’∪B’

m ∈Y

hence, X∈Y………………..(i)

now let n be the arbitrary element of Y so, n∈Y

which means n ∈A’∪B’

n A’ and n∈B’

n∈A and n∈B

n(A∩B)

n (A∩B)’

n∈Y

hence Y∈X………………..(ii)

from equation (i) and(ii)

(A∩B)’ = A’ B’

DE MORGAN’S LAW ON DIFFERENCES IN SET THEORY

This is also known as the Second law of de morgan’s theorem which says that the 

For any three sets A,B and C

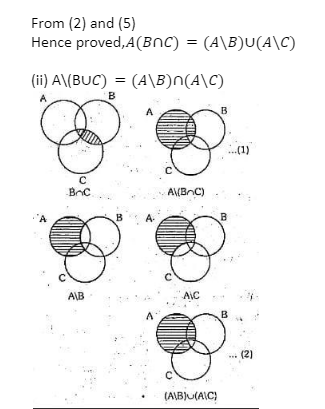
(i)A\(B∪C)=A\B∩(A\C)

(ii)A(B∩C)=A\B∪(A\C)

PROOF OF DE MORGAN’S LAW ON DIFFERENCES BY VENN DIAGRAM

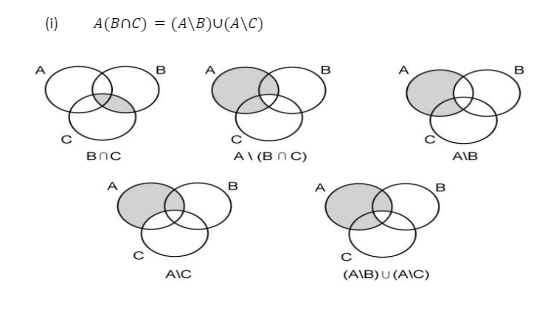
Hence prove that

at A\(B∪C)=A\B∩(A\C)

EXAMPLE OF DE MORGAN’S LAW ON DIFFERENCE 

Example 1: Let A={a,b,c,d,e,f,g,x,y,z}

B={1,2}

C={d,e,f,g,2,y}

B∪C={1,2,c,d,e,f,g,y}

A\(B∪C)={a,b,x,z}

A\B ={a,b,f,g,x,y,z}

A\C = {a,b,c,x,z}

(A\B)∩(A\C) = {a,b,x,z}

Hence A\(B∪C)=A\B∩(A\C)

Let A= {10,15, 20, 25, 30, 35, 40, 45, 50}

B = {1, 5,10,15, 20, 30} 

C = {7, 8,15,20,35,45, 48}.

B u C  =  { 1, 5, 7, 8, 10, 15 , 20,30, 35, 45, 48 }

A / (B u C)  =  { 25, 40, 50 }

A\B= {25, 35, 40, 45, 50}

A\C= {25, 30, 40, 50}

(A\B) U (A\C) = { 25, 40, 50} 

Hence  proved A\(B n C)  =  (A\B)u(A\C)

CONCLUSION

In this article we learn the de morgan’s theorem statement and its proof in set theory and  our main focus in on the de morgan’s law on differences which say that theorem which says that the For any three sets A,B and C

(i)A\(B∪C)=A\B∩(A\C)

(ii)A(B∩C)=A\B∪(A\C)

 we talk about the statement of de morgan’s law on differences  and its proof in set theory by venn diagram as well as by taking examples and also  do some examples so that it will clear better and solve some questions based on de morgan’s law on differences.